Modèles de Structures Aléatoires de Type Réaction-Diffusion - Thèse de Morphologie Mathématique - Luc Decker, Ecole des Mines de Paris (1999)

suivant: 2. Modèles de diffusion remonter: 1. Approche macroscopique de précédent: 1.3 Equation de la [Table des matières]

1.4 Modèle de diffusion par différences finies

Il s'agit d'intégrer l'équation de la diffusion en tout point d'un domaine en deux ou trois dimensions. Ce domaine est discrétisé sous la forme d'un réseau régulier de sites en trame carrée ou cubique, donc avec des relations de voisinage en connexité 4 ou 8 en 2D, 6 ou 26 en 3D. A tout site, on associe une concentration locale C(x,y,z,t), représentée sous la forme d'un nombre flottant. L'équation de la diffusion est ré-écrite sous la forme d'une différence finie. Nous commencerons par en rappeler les principes à une dimension :

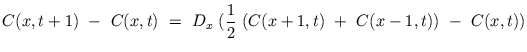$\displaystyle C(x,t+1)\ -\ C(x,t) \ = \ D_{x}\ ( \frac{1}{2}\ (C(x+1,t)\ +\ C(x-1,t))\ - \ C(x,t))$

(II.-4)

L'expression du membre de droite correspond à la discrétisation de l'opérateur Laplacien. On exprime alors directement en fonction de :

$\displaystyle C(x,t+1)\ = (1 - D_{x})\ C(x,t)\ +\ \frac{D_{x}}{2}\ (C(x+1,t)\ +\ C(x-1,t))$

(II.-5)

En un procédé itératif, on définit ainsi l'évolution élémentaire et simultanée en tout site du domaine. Dans l'évolution de la concentration au point , on distingue un premier terme qui correspond à sa diminution par la perte d'une partie de la matière ( $D_{x} \ C(x,t)$ ) qui se trouvait en , alors qu'un deuxième terme représente les apports de matière en provenance du voisinage du point . Un équilibre tend à s'instaurer de sorte que lorsqu'il y a égalité des concentrations . La validité de cet opérateur de diffusion a été vérifiée par l'étude de profils gaussiens résultants de l'amortissement (et de la dispersion) progressif d'une impulsion locale. Par ailleurs, il s'agit d'un opérateur linéaire, que l'on peut implanter sous la forme d'une convolution spatiale par un masque centré en et couvrant le voisinage de (, à une dimension).

Pour des raison de stabilité numérique du modèle, il est impératif que $1 - D_{x} \geq 0$ : la dimution de la concentration au point ne doit pas dépasser sa valeur initiale. Dans le cas contraire, des oscillations (ou erreurs) numériques se trouvent amplifiées. En conséquence, les coefficients de diffusion applicables varient entre 0 et . Il s'agit de coefficients relatifs, propres au modèle; il peuvent être exprimés en ${pixels}^2 {[T]}^{-1}$ ou ${voxels}^2 {[T]}^{-1}$ .

Par ailleurs, un phénomène de parité peut apparaître lorsque ; dans ce cas, dépend uniquement des concentrations voisines et ( est indépendant de ). Il en résulte une décomposition du domaine en sous-domaines indépendants et entrecroisés qui évoluent sans aucun échange d'information. Au temps temps pair, l'un des sous-domaines sera décrit par avec entier; au temps impair, il se trouvera en . Ce phénomène peut être affecté par les conditions aux limites du domaine. En cas de limites périodiques, il y a couplage entre les sous-domaines lorsque le nombre de sites est impair.

Ces principes restent valables dans des dimensions supérieures; le phénomène de parité se traduit par des effets de "damiers" en 4-connexité (ou 6-connexité en 3D). Cependant, ce problème peut à présent être contourné en intégrant les seconds voisins dans le voisinage d'un site - soit des relations de 8-connexité (en 2D) ou de 26-connexité (en 3D). Dans ce cas, les concentrations diffusent à travers un domaine unique, même lorsque . On utilisera ainsi un noyau de convolution $3 \times 3$ en 2D (ou en 3D, $3 \times 3 \times 3$ ). En trois dimensions, si $N_{26}$ représente l'ensemble des translations $h(h_{x},h_{y},h_{z})$ décrivant le voisinage 26-connexe d'un site, l'équation II-5 devient:

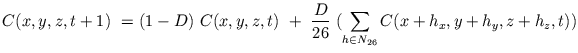$\displaystyle C(x,y,z,t+1)\ = (1 - D)\ C(x,y,z,t)\ +\ \frac{D}{26}\ (\sum_{h \in N_{26}} C(x+h_{x},y+h_{y},z+h_{z},t))$

(II.-6)

lorsque la diffusion est isotrope, avec un unique coefficient de diffusion . Une variante possible consiste à attribuer des pondérations différentes en fonction du niveau de voisinage (6 "premiers" voisins, 12 "seconds" voisins et 8 "troisièmes" voisins).

Optimisations
Nous traiterons ici le cas de l'opérateur de diffusion en trois dimensions; les principes restent semblables en deux dimensions. Le noyau de convolution utilisé pour l'opérateur de diffusion ne contient que deux pondérations différentes ( au centre, et pour le voisinage). Cette opération peut donc être optimisée par une méthode classique, dite de la fenêtre glissante. On remarque en effet que dépend en partie de . La convolution est réalisée en balayant l'image par un masque cubique $3 \times 3 \times 3$ , dans l'ordre des directions croissantes . Lorsque le masque se déplace d'un site dans la direction , seuls nouveaux points sont couverts par le masque, et points en sortent - la valeur de ces points ayant été conservée. Il en résulte qu'il n'est pas nécessaire de parcourir voisins en chaque site. Par ailleurs, l'opération de convolution pourrait aussi être décomposée selon les trois directions de l'espace, en raison de la forme gaussienne du noyau de convolution. Cependant, il serait alors nécessaire de balayer trois fois l'image par un masque à une dimension, orienté successivement dans les directions , et . Sur le plan pratique, il semble que la multiplication des accès aux données ne soit pas avantageuse, en particulier en trois dimensions, en raison du mode de gestion de la mémoire vive dans les architectures matérielles usuelles. Enfin, la convolution est effectuée "en place", sans recourir à un autre domaine pour y enregistrer son résultat; il est cependant nécessaire d'utiliser une image temporaire bidimensionnelle pour y placer les valeurs du plan en cours de traitement, avant qu'elles ne soient mises à jour. Cette image est alors utilisée lorsque le plan vient à être balayé.