suivant: 2.3 Automates cellulaires remonter: 2. Modèles de diffusion précédent: 2.1 Systèmes à base [Table des matières]
Dans la théorie du Mouvement Brownien, on considère qu'un fluide est
constitué de particules élémentaires, qui disposent de leur propre
liberté de mouvement. A l'échelle la plus réduite, il s'agit de
molécules. Mais ce concept reste valide à plus grande échelle, et sert de base
à une classe de modèles de fluides. Les particules engendrent un comportement
collectif (ou moyen), qui est caractérisé au niveau macroscopique par des statistiques
sur les grandeurs mesurables pour chaque particule isolément. On considère
ainsi la résultante des contributions des particules élémentaires, qui forment
une population représentative du fluide, dans toute sa variabilité. On peut y voir
une application du célèbre théorème de la Limite Centrale : la somme
de variables aléatoires indépendantes suit une loi normale.
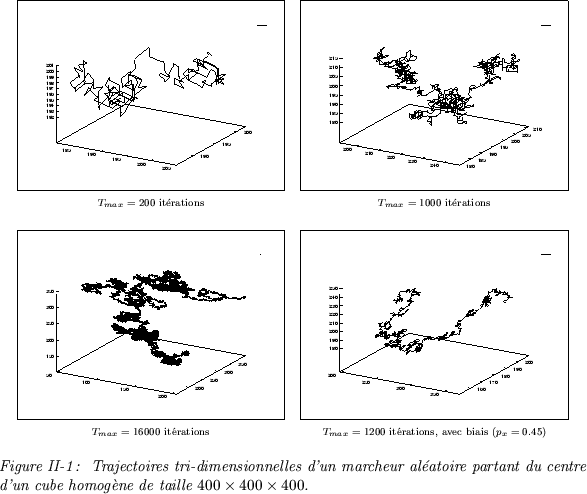
Selon une approche lagrangienne, on va s'intéresser à la trajectoire d'une particule
individuelle en fonction du temps. Dans son mouvement aléatoire désordonné,
la particule participe au processus de diffusion du fluide. Dans le cas
présent, on ne cherchera pas à reproduire la cause de ce mouvement brownien,
c'est à dire les collisions ou interactions avec d'autres particules.
Du point de vue des simulations, introduisons
la notion de marcheur aléatoire :
une particule dont la direction de déplacement change aléatoirement à chaque pas
de temps. Cette approche ne relève pas du même principe que les systèmes de
particules. D'une part, parce les trajectoires des particules sont simulées une
par une. D'autre part parce que l'objectif final est d'obtenir des mesures
quantitatives sur le fluide simulé. Les conditions aux limites influencent
le comportement du fluide, comme par exemple dans le cas d'un milieu poreux.
Inversement, les mesures portant sur la diffusion du fluide - la dispersion
des particules - constituent un outil pour caractériser le milieu traversé.
![$\displaystyle \hspace{-1cm} \left\{ \begin{array}{l} P[x' = x(t) + 1] = p_{x}\ ...
...z}}\ \ P[z' = z(t) - 1] = 1 - p_{z} - p_{o_{z}}\\ \end{array} \right. \ \ \ \ $](img209.gif) |
(II.-7) |
| (II.-8) |
| (II.-9) |
Les marcheurs aléatoires ainsi définis se déplacent sur une trame cubique. Par
combinaison des mouvements autorisés dans chaque direction, il existe ![]() déplacements unitaires possibles pour une particule à condition que les
probabilités d'immobilisation
déplacements unitaires possibles pour une particule à condition que les
probabilités d'immobilisation ![]() ,
, ![]() et
et ![]() soient non nulles. Cette valeur correspond à la connexité de la trame:
chaque point admet 26 voisins. Une particule peut aussi rester immobile avec
la probabilité
soient non nulles. Cette valeur correspond à la connexité de la trame:
chaque point admet 26 voisins. Une particule peut aussi rester immobile avec
la probabilité
![]() . Par ailleurs, les
probabilités
. Par ailleurs, les
probabilités ![]() ,
, ![]() et
et ![]() permettent d'introduire une dérive
dans les déplacements des particules. Pour que ces déplacements soient symétriques dans
chaque direction,
il faut que les probabilités de déplacements positifs
permettent d'introduire une dérive
dans les déplacements des particules. Pour que ces déplacements soient symétriques dans
chaque direction,
il faut que les probabilités de déplacements positifs ![]() et négatifs
et négatifs ![]() soient égales, d'où
soient égales, d'où
La vitesse moyenne ![]() d'une particule
d'une particule ![]() au cours de sa trajectoire s'achevant au
temps
au cours de sa trajectoire s'achevant au
temps ![]() est estimée par
est estimée par
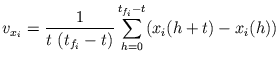 |
(II.-10) |
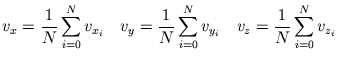 |
(II.-11) |
| (II.-12) |
Soient ![]() ,
, ![]() et
et ![]() les coefficients de diffusion
du fluide à travers le milieu poreux, pour les trois directions.
Ces coefficients macroscopiques sont définis pour
un milieu homogène équivalent. Leur estimation
est obtenue par l'une ou l'autre des méthodes suivantes, qui exploitent
les statistiques des trajectoires des marcheurs aléatoires: [Matheron79,Jeulin92a,Akoulenko95]
les coefficients de diffusion
du fluide à travers le milieu poreux, pour les trois directions.
Ces coefficients macroscopiques sont définis pour
un milieu homogène équivalent. Leur estimation
est obtenue par l'une ou l'autre des méthodes suivantes, qui exploitent
les statistiques des trajectoires des marcheurs aléatoires: [Matheron79,Jeulin92a,Akoulenko95]
![$\displaystyle D_{x} \ t = \frac{1}{2} E[X_{h+t} - X_{h} - v_{x} t]^{2}$](img238.gif) |
(II.-13) |
![$\displaystyle \gamma(t) = \frac{1}{2} E[X_{h+t} - X_{h}]^{2}$](img240.gif) |
(II.-14) |
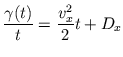 |
(II.-15) |
Dans le cas particulier où les particules se déplacent dans un espace homogène, on obtient les valeurs de référence des coefficients de diffusion en fonction des probabilités de la marche aléatoire:
| (II.-16) |
Diffusion non-fickienne. Pour certaines catégories de milieux poreux, la diffusion n'obéit pas à la loi de Fick. C'est même une situation couramment observée dans l'étude de problèmes concrets, pour lequels la loi de Fick est une simple approximation. La morphologie complexe d'un milieu poreux est à l'origine de non-linéarités, par exemple lorsque ce dernier renferme des cavités sans issues, qui jouent le rôle de "pièges" à une échelle donnée et peuvent être contournées à une échelle plus grande. Si l'estimation de la diffusion par marcheurs aléatoires reste valable, la relation qui relie le variogramme des trajectoires et le coefficient de diffusion prend la forme suivante pour certains types de diffusion :
![$\displaystyle D_{x} \ t^{\alpha} = \frac{1}{2} E[X_{h+t} - X_{h} - v_{x} t]^{2}\ \ \ \ \ $](img246.gif) avec avec |
(II.-17) |
| (II.-18) |
![$\displaystyle P[X(t) \geq a] = \frac{1}{\sqrt{4 \pi D_{x} t}} \int_{a}^{\infty} e^{- \frac{(x - v_{x} t)^2}{4 D_{x} t}} dx$](img256.gif) |
(II.-19) |
soit
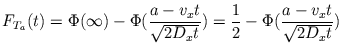 |
(II.-20) |
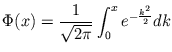 |
(II.-21) |
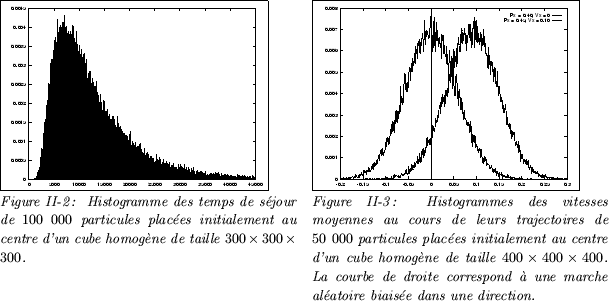
Remarquons que cette méthode ne s'applique pas dans le cas où une partie des temps de séjour des particules sont infinis, lorsque certaines particules restent captives dans les porosités qui ne communiquent pas avec l'extérieur. Notons aussi que cette méthode permet d'estimer un coefficient de séjour pour des temps longs et pour de grandes échelles de porosité, ce qui correspond à la méthode physique de mesure d'un coefficient de diffusion par l'intermédiaire d'un traceur traversant l'échantillon.
Enfin, la mise en place de parois étanches sur les bords du domaine, dans une ou deux directions, permet de mesurer les temps de séjour dans les directions restantes sans être confronté au problème des sorties des particules par un autre bord que celui qui est fixé pour la mesure, même quand la dérive de la marche aléatoire est réduite. L'intéret de fermer ainsi une partie des bords du domaine apparait surtout lorsque la taille du domaine dans une direction est très inférieure à ses dimensions dans les autres directions. On constate que dans le cas de parois latérales étanches, les distributions théoriques et expérimentales des temps de séjour restent en correspondance.
La détection des porosités par traitement d'image
constitue la première étape de l'étude, que nous ne détaillerons pas ici.
L'exploitation des clichés a posé de nombreuses difficultés, en raison de leur
qualitité médiocre. L'échantillon a ensuite été reconstitué dans une image
binaire tri-dimensionnelle, par mise en correspondance des sections consécutives.
La fraction volumique totale des pores est de l'ordre de 22%.
Dans ce milieu poreux virtuel, un test de percolation a tout d'abord
été réalisé afin de vérifier
qu'il existait bien un chemin entre faces permettant de le traverser. Dans ce but, un
algorithme de propagation géodésique a été appliqué [Jeulin92b,Demarty96].
Les porosités ouvertes sur l'extérieur de l'échantillon sont également détectées
par cet algorithme; leur volume représente 88% de l'ensemble des porosités : le
milieu poreux est fortement interconnecté (Figure II-5).

Finalement, des simulations de marcheurs aléatoires sont effectuées
dans les porosités ouvertes afin de déterminer les coefficients de
diffusion d'un milieu homogène équivalent, dans les directions ![]() et
et ![]() .
D'une part, la méthode du variogramme donne une estimation à petite échelle, avec des
distances moyennes parcourues par les marcheurs aléatoires de l'ordre de
.
D'une part, la méthode du variogramme donne une estimation à petite échelle, avec des
distances moyennes parcourues par les marcheurs aléatoires de l'ordre de ![]() pour
pour
![]() itérations; pour des temps plus longs, une partie des marcheurs
sortent en effet du domaine. Dans la direction horizontale
itérations; pour des temps plus longs, une partie des marcheurs
sortent en effet du domaine. Dans la direction horizontale ![]() , la diffusion respecte
la loi de Fick et on obtient un rapport
, la diffusion respecte
la loi de Fick et on obtient un rapport
![]() ,
, ![]() étant le coefficient de diffusion de référence pour un milieu totalement
poreux. La Figure II-6 présente le variogramme des trajectoires
dans la direction verticale; comme ce dernier n'est pas linéaire, on
formule l'hypothèse que la loi de Fick n'est pas vérifiée. En conséquence,
une loi de diffusion de type
étant le coefficient de diffusion de référence pour un milieu totalement
poreux. La Figure II-6 présente le variogramme des trajectoires
dans la direction verticale; comme ce dernier n'est pas linéaire, on
formule l'hypothèse que la loi de Fick n'est pas vérifiée. En conséquence,
une loi de diffusion de type
![]() est appliquée pour obtenir
un ajustement avec une loi théorique; la méthode usuelle des "moindres
carrés" est mise en oeuvre pour estimer simultanément
est appliquée pour obtenir
un ajustement avec une loi théorique; la méthode usuelle des "moindres
carrés" est mise en oeuvre pour estimer simultanément ![]() et
et ![]() .
D'autre part, la méthode des temps
de séjour donne des coefficients de diffusion plus élevés à grande échelle,
lorsque l'interconnection tri-trimensionnelle du milieu poreux intervient
davantage. L'analyse des résultats permet aussi
de vérifier l'anisotropie du milieu poreux étudié: le coefficient de
diffusion est cinq fois plus faible dans la direction
.
D'autre part, la méthode des temps
de séjour donne des coefficients de diffusion plus élevés à grande échelle,
lorsque l'interconnection tri-trimensionnelle du milieu poreux intervient
davantage. L'analyse des résultats permet aussi
de vérifier l'anisotropie du milieu poreux étudié: le coefficient de
diffusion est cinq fois plus faible dans la direction ![]() orthogonale
aux porosités lamellaires.
orthogonale
aux porosités lamellaires.
 Decker, Luc. "Modèles de structures aléatoires de type réaction-diffusion". PhD diss. (191 p.), Paris, ENSMP-CMM, 1999.
Decker, Luc. "Modèles de structures aléatoires de type réaction-diffusion". PhD diss. (191 p.), Paris, ENSMP-CMM, 1999.