Modèles de Structures Aléatoires de Type Réaction-Diffusion - Thèse de Morphologie Mathématique - Luc Decker, Ecole des Mines de Paris (1999)

suivant: 3.3 Extensions et développements   remonter: 3. Les Gaz sur   précédent: 3.1 Introduction   [Table des matières]

3.2 Le modèle FHP

Remarque préliminaire: il existe différentes variantes du modèle FHP, selon le nombre $n$ de cellules contenues dans chaque noeud (ou site) du réseau; nous décrirons ici le modèle FHP-III, qui correspond à $n = 7$.

Structure du modèle
Le modèle FHP est construit sur un réseau régulier hexagonal, à deux dimensions. Il décrit l'évolution d'une population de particules élementaires, toutes semblables, dont les déplacements sont contraints par ce réseau. Pour chaque particule, il existe 7 états possibles : une vitesse unitaire orientée dans l'une des 6 directions isotropes du réseau hexagonal, soit $c_{i}$ avec $i \in \{1, ..., 6\}$ ou une vitesse nulle $c_{0}$. Comme dans un automate cellulaire, nous utiliserons par la suite le terme de cellule pour désigner chacune de ces vitesses possibles $c_{i}$. Tout noeud du réseau est ainsi constitué de 7 cellules. Dans un Gaz sur Réseau, la règle qui impose que chaque cellule contienne au plus une particule s'applique sous l'appellation de principe d'exclusion. Comme les cellules sont liées aux directions de déplacement, au plus une particule peut se déplacer d'un noeud $x$ du réseau vers un noeud précis de son voisinage immédiat, noté $x + c_{i}$, où la direction $i \in \{1, ..., 6\}$ est fixée.

Opérateurs de transformation : cycle élémentaire
D'une part, à chaque pas de temps élémentaire (ou itération), toutes les particules en mouvement se déplacent vers le noeud voisin le plus proche dans la direction $i$ associée à leur vitesse $c_{i}$, ce qui définit l'action d'un opérateur local de translation $T$.

D'autre part, un opérateur local de collision $C$ va traiter des interactions entre particules localisées en un même noeud du réseau. Des règles de collision microdynamiques vont ainsi redistribuer les vitesses des particules à chaque itération en respectant les contraintes de conservation de la masse totale - donc du nombre de particules - et de la quantité de mouvement en chaque noeud. L'opérateur $C$ réalise une diffusion isotrope des particules, à condition que leur densité soit suffisante pour engendrer des collisions. Il s'agit d'un opérateur "naturellement" aléatoire : lorsque différentes configurations sont possibles pour la redistribution des vitesses, un tirage aléatoire équi-probable est effectué. Toute particule d'un gaz sur réseau peut jouer le rôle de marcheur aléatoire, auquel est applicable la théorie introduite au chapitre précédent (2.2) pour l'estimation des coefficients de diffusion.

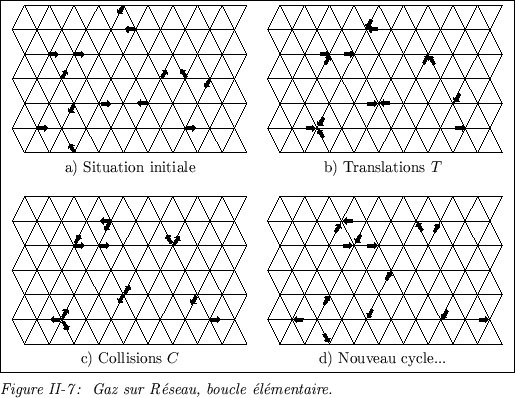
Comme l'illustre la Figure II-7, un cycle d'évolution du système consiste en la composition des opérateurs de translation et de collision entre particules, soit $C \circ T$. Le choix de règles de collisions spécifiques détermine la viscosité du fluide ainsi modélisé; nous donnons les règles précises du modèle FHP-III sur la Figure II-8. Ces règles sont enregistrées dans une look-up table, qui utilise la configuration binaire d'un noeud avant collision comme clé d'entrée.

Conditions aux limites
Le traitement des conditions aux limites est également local, donc à un niveau microscopique. En particulier, les particules qui rencontrent un obstacle subissent un rebond élastique en remplacement des règles de collision déjà évoquées. Il en résulte qu'une carte des obstacles est introduite dans le modèle en tant qu'image binaire. Plus précisément, un obstacle est caractérisé par sa frontière, constituée par les sites du réseau où le sens de déplacement des particules est inversé au contact de l'obstacle. La définition de telles frontières suffit à conserver les particules à l'extérieur des obstacles. Dans ces conditions, la morphologie des obstacles est évidemment quelconque: nous ne manquerons pas d'exploiter cet atout majeur des gaz sur réseau. Par ailleurs, des conditions périodiques sont fréquemment imposées aux bords du champ de simulation, ce qui engendre un espace de topologie torique.

Hydrodynamique
Il a été démontré qu'à l'échelle macroscopique, les vitesses de ce fluide respectent les équations de Navier-Stockes dans la limite d'incompressibilité [Frisch86]. A deux dimensions, ce point se vérifie pour tous les Gaz sur Réseau construits sur des réseaux hexagonaux, soient les modèles FHP.

Pour illustrer la nature hydrodynamique du modèle FHP, nous avons reproduit l'expérience d'un écoulement perturbé par une plaque mince. Sur la Figure II-9, on observera nettement les tourbillons qui sont apparus spontanément à l'arrière de l'obstacle. Il s'agit en quelque sorte d'une auto-organisation du transport des particules : des structures macroscopiques apparaissent à partir de règles d'évolution purement locales. Selon les auteurs du modèle FHP, ce dernier est capable de reproduire des comportements non-linéaires de manière bien plus précise que les équations de Navier-Stockes, qui constituent une approximation macroscopique de la dynamique d'un fluide.

suivant: 3.3 Extensions et développements   remonter: 3. Les Gaz sur   précédent: 3.1 Introduction   [Table des matières]

Decker, Luc. "Modèles de structures aléatoires de type réaction-diffusion". PhD diss. (191 p.), Paris, ENSMP-CMM, 1999.