L.Decker-Thèse ENSMP 1999-4.5 Modèle complexe de Ginzburg-Landau

$\begin{displaymath}\begin{array}{ll}\frac{\partial Z}{\partial t} \ = \ D \bigtr... ... B = \beta \ + \ i \ \delta \\ \end{array} \right. \end{array}\end{displaymath}$

(III.-26)

$\displaystyle \left\{ \begin{array}{ll} \frac{\partial Z_{1}}{\partial t} \ = \... ...\vert Z \right\vert}^{2} \ = \ {Z_{1}}^2 \ + \ {Z_{2}}^2\\ \end{array} \right.$

(III.-27)

**Figure:** Simulations 2D par éléments finis du modèle complexe de Ginzburg-Landau. Domaines $600 \times 600$ . Paramètres communs: $Z_{1}(x, t=0) \approx 0.0$ , $Z_{2}(x, t=0) \approx 0.0$ , $\alpha = 1.0$ , $\beta = 1.0$ , $\gamma = 1.0$ , $K_{r} = 0.10$ . Concentrations $Z_{1}$ représentées en fausses couleurs (sauf indication contraire).
**Figure:** Modèle complexe de Ginzburg-Landau : tracés spatio-temporels (en fausses couleurs) de profils de la concentration $Z_{1}$ . Le temps s'écoule de gauche à droite. Domaines $400 \times 400$ . Autres paramètres: voir Figure III-40.
$\begin{figure} \centerline {\begin{tabular}{ccc} \fbox{\epsfxsize=4.5cm \epsfbox... ...) $\delta = 1.4$, $0 < t < 1400$\ : mode oscillant\\ \end{tabular}}\end{figure}$

Des ondes spirales sont solutions de cette équation, avec des comportements oscillants qui correspondent à une possible rotation des spirales sur elles-même. Dans la réalité, de telles structures peuvent effectivement apparaitre, en particulier au sein de cristaux liquides nématiques soumis à des champs electro-magnétiques; pour plus de détails, on consultera par exemple les travaux de l'équipe de P. Coullet [Frisch94]. Depuis plus d'une dizaine d'années, les ondes spirales font ainsi l'objet de très nombreux recherches, aussi bien théoriques [Hagan82] que pratiques (simulations et expérimentations).

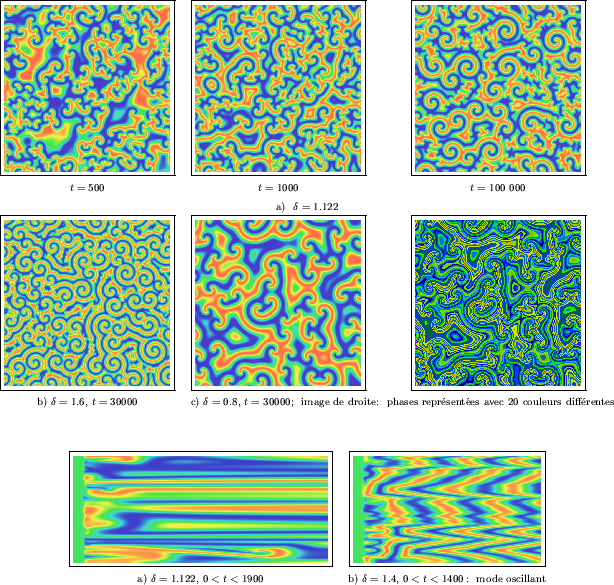
En deux dimensions, essayons d'expliquer la dynamique de ce système de réaction-diffusion à partir de nos observations. La Figure III-40a montre trois étapes d'une simulation, le domaine ayant été initialisé avec un bruit blanc. Après

itérations (image de gauche), l'émergence d'une population hétérogène de structures spirales peut s'observer - le milieu est extrêmement désordonné. Ces spirales se répartissent en deux populations: d'une part, des spirales simples qui présentent de beaux enroulements; d'autre part, des spirales doubles (à deux branches) de plus petites tailles. Pour

, tout le domaine a été envahi par les branches des spirales. Simultanément, une sélection s'est opérée: les spirales doubles les plus petites ont disparu, en s'effrondrant brutalement. Ces phénomènes laissent temporairement leur marque dans le système sous la forme de structures ovales concentriques, les "ondes de l'explosion" en quelque sorte. Sur l'image des concentrations pour

, on en trouve deux exemples: l'un près du bord gauche au centre, l'autre intersecte le bord inférieur. Sur l'image précédente (pour

), on vérifiera que les régions correspondantes sont toutes deux occupées par des spirales doubles très resserrées. Le mécanisme de disparition d'une spirale double est assez simple: ses deux centres se rapprochent de plus en plus rapidement; puis la structure "explose" lorsqu'ils se rencontrent, comme s'ils portaient des charges opposées. La dynamique d'une telle paire de vortex a déjà fait l'objet de nombreux travaux théoriques (voir par exemple [Wu91]). Les spirales doubles de grande taille (aux centres bien écartés) ont ainsi une durée de vie plus longue. Les spirales grandissent et se déplacent lentement à travers l'espace; après

itérations (image de droite), le milieu semble bien mieux organisé qu'à

itérations. De fait, les spirales représentent autant de cellules en interaction, qui sont chacune à l'origine d'une zone d'influence. Lorsqu'une cellule disparaît, l'espace qu'elle occupait est ainsi partagé entre les cellules voisines, en fonction de leur importances respectives. Les déplacements des cellules s'expliquent également par cette compétition pour un espace "vital" : l'apparition d'un espace libre va attirer les cellules voisines, puis les réorganisations spatiales se propagent à travers tout le domaine.

Le paramètre $\delta$ contrôle de nombreux aspects du modèle. Pour $\delta = \delta_{c} = 1.122 \ \pm 0.001$ (déterminé expérimentalement dans notre cas), le milieu n'est pas en oscillation. Dans la situation contraire, les spirales sont en rotation; les deux parties d'une spirale double tournent ainsi en sens contraires. Sur la Figure III-40, on percevra aisément les différences de morphologies selon la valeur de $\delta$ par rapport à $\delta_{c}$ . Pour $\delta > \delta_{c}$ , les branches des spirales sont fines et allongées, permettant même la présence de spires multiples dans certains cas (image b). Au contraire, pour $\delta < \delta_{c}$ , leurs branches sont épaisses et les enroulements peu marqués (image c). Indépendamment de leur sens de rotation, nous avons constaté que les spirales se déroulent pour $\delta > \delta_{c}$ , et qu'elles s'enroulent pour $\delta < \delta_{c}$ . Seule l'observation de séquences vidéo nous a permis d'étudier le phénomène. Dans un mouvement d'enroulement, la matière est aspirée par le centre de la spirale, et les branches sont compressées vers l'intérieur. Au contraire, le déroulement se traduit par l'émission de matière à partir du centre, et les branches sont étirées vers extérieur, ce qui peut expliquer les différences d'aspects observées. Par ailleurs, les interactions entre spirales sont mises en évidence sur l'image des phases du modèle (Figure III-40c, à droite) qui a été obtenue en représentant

(à valeurs entre 0 et $2 \pi$ ) sur 20 niveaux à l'aide de couleurs distinctes. Le résultat permet d'observer les lignes d'égale phase (iso-phases) qui relient les centres des spirales. Comme pour les modèles précédents, des tracés spatio-temporels ont été produits. L'analyse d'une section uni-dimensionnelle s'avère difficile pour des structures aussi complexes que sont les spirales. Sur la Figure III-41a, la disparition d'une spirale a cependant laissé une intéressante trace en forme de cône (en bas à droite). Lorsque les spirales sont en rotation, le profil spatio-temporel rend bien compte des oscillations périodiques associées (Figure III-41b). Les lignes rouges correspondent par exemple aux instants où la concentration $Z_{1}$ est maximale. Si le milieu était homogène, elles seraient parfaitement verticales. Dans le cas présent, elles sont sinueuses parce qu'il existe un déphasage dans l'évolution des points de ce profil. Tout point du profil se trouve ainsi périodiquement à une concentration maximale, mais à des instants différents en raison de la propagation spatiale de l'onde chimique.

La partition du domaine en cellules peut être clairement établie grâce aux images du module ${\left\vert Z \right\vert}^{2}$ (voir Figure III-42 pour

, et Figure III-43a). Sur ces images, les centres des spirales correspondent à de profonds minima quasi-ponctuels (points bleus), alors que leurs enveloppes (ou frontières) sont aussi mises en évidence parce qu'elles coïncident avec les plus fortes valeurs du module (en orange). Les frontières des cellules sont semblables à un squelette. De plus, elles sont plus ou moins marquées : il existe ainsi des groupes de cellules dont les frontières internes sont à peine visibles. C'est par exemple le cas des paires de cellules associées à des spirales doubles. L'image du module montre que le modèle de Ginzburg-Landau permet d'obtenir également des partitions aléatoires de l'espace, aux propriétés sans doute particulières (et qui restent à étudier).

**Figure:** Simulation 2D du modèle complexe de Ginzburg-Landau : évolution du module ( ${Z_{1}}^2 + {Z_{2}}^2$ ) durant la génèse des ondes spirales. Domaine $600 \times 600$ , $Z_{1}(x, t=0) \approx 0.0$ , $Z_{2}(x, t=0) \approx 0.0$ . Paramètres: $\alpha = 1.0$ , $\beta = 1.0$ , $\gamma = 1.0$ , $\delta = 1.5$ , $K_{r} = 0.05$ . Représentation en fausses couleurs (pour $t \geq 200$ , les points bleus correspondent à de profonds minimas locaux).
**Figure:** *Modèle complexe de Ginzburg-Landau: exploitations possibles de l'image du module. Réalisation identique à celle de la Figure III-40a.*
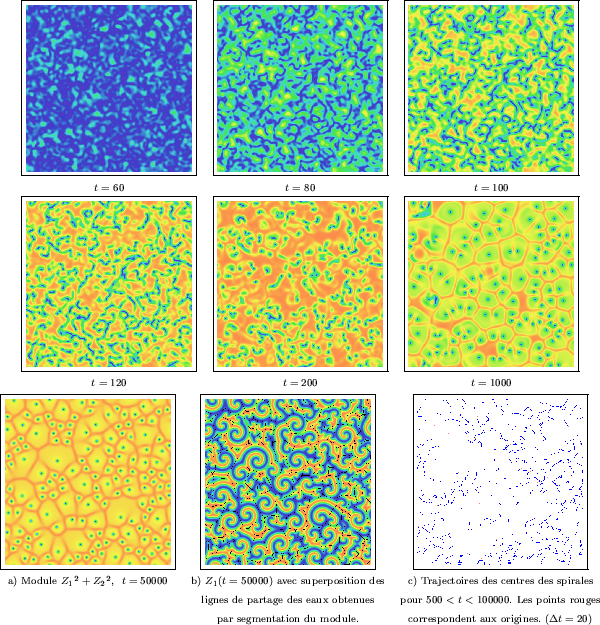$\begin{figure} \centerline {\begin{tabular}{ccc} \fbox{\epsfxsize=4.5cm \epsfbox... ...size correspondent aux origines. ($\Delta t = 20$)\\ \end{tabular}}\end{figure}$

A partir de l'image ${\left\vert Z \right\vert}^{2}$ , nous avons également cherché à comprendre comment les spirales prennent naissance à partir d'un bruit blanc, au tout début d'une simulation. Sur la Figure III-42, on observe la génèse des centres des spirales - aussi appelés singularités de phase - pour $t \leq 200$ . Les images pour

itérations sont les plus intéressantes: elles montrent l'existence éphémère de lignes sinueuses et discontinues (en forme de "vers"), qui s'entrecroisent à travers le milieu. Ces lignes s'amincissent ensuite et leur longueur diminue. Finalement, des points isolés ou de courts segments demeurent pour

: la croissance des spirales va alors débuter à partir de ces centres.

L'image du module a encore été exploitée de deux manières. D'une part, les cellules peuvent être segmentées par la méthode de la ligne de partage de eaux (LPE), comme dans le cas du Brusselator. Un seuillage à faible niveau de l'image du module permet d'obtenir un marqueur unique par cellule, puis l'algorithme de la LPE est directement appliqué sur le relief constitué par l'image du module. Les frontières peuvent alors être incrustées dans l'image $Z_{1}$ qui contient les structures spirales (Figure III-43b). Ce résultat est intéressant, parce qu'il n'existe pas de méthode pour délimiter directement les spirales dans l'image $Z_{1}$ (ne connaissant que le résultat final, il serait difficile de concevoir de quelle manière il a été obtenu). D'autre part, il est possible de mesurer les trajectoires des centres des cellules, à condition qu'ils soient déterminés en tant que points précis. Comme pour les marqueurs des cellules, le module est seuillé de façon à produire un grain peu étendu pour chaque minimum. Puis ces grains sont identifiés tels des composantes connexes. Enfin, les centres recherchés correspondent aux barycentres de ces composantes connexes. La Figure III-43c montre un exemple de trajectoires obtenues durant

itérations. Les déplacements des spirales paraissent chaotiques: on assiste à des "boucles", et autres "demi-tours"; en fait, ils traduisent l'histoire complexe du milieu, qui a notamment été marquée par la disparition de nombreuses cellules. A ce sujet, on observera quelques trajectoires de centres de spirales doubles. Ils apparaissent en forme de "V" : ces centres qui vont par paires suivent des mouvement symétriques puis se rejoignent; les centres voisins ont alors été attirés par l'espace libéré.

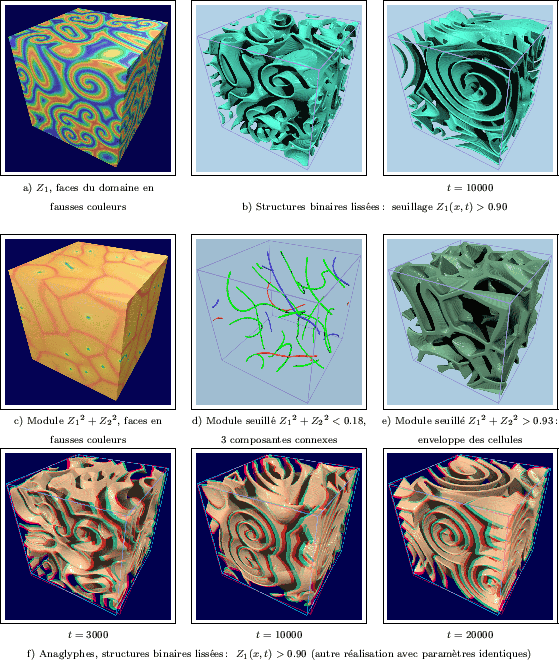
[] [] Nous achèverons cette présentation du modèle complexe de Ginzburg-Landau par quelques simulations en trois dimensions. Si la dynamique du système reste inchangée par rapport aux réalisations bidimensionnelles déjà analysées, la morphologie des structures change quelque peu. Dans une dimension supérieure, les coupes du milieu renferment toujours des structures spirales similaires à celles qui sont obtenues en deux dimensions. Les faces d'un domaine sont ainsi présentées sur Figure III-44a. Par contre, après binarisation du milieu, on constate en fait que les spirales deviennent des rouleaux, sous la forme d'enroulements inscrits à l'intérieur de tores. La Figure III-44 (images b et f) en donne plusieurs exemples. La croissance des structures, associée aux limites périodiques du domaine simulé, finit par engendrer un milieu dans lequel les rouleaux ne sont plus reconnaissables (Figure III-44b, image de droite). Il semble que les conditions aux limites périodiques utilisées dans toutes nos simulations jouent un rôle important dans ce type de dégénérescence. L'image du module (Figure III-44c) permet également de mieux appréhender la structure du milieu. Les minima du module ne sont plus ponctuels: il se présentent sous la forme de tores entremèlés, où chaque tore correspond à l'axe central d'un rouleau (voir Figure III-44c). Pour les domaines de $200^{3}$ voxels que nous avons utilisés, le nombre de rouleaux distincts est très faible (sur l'exemple présenté, il n'y a ainsi plus que trois rouleaux après

itérations). En trois dimensions, l'interconnection des structures s'avère toujours plus importante; cette règle s'applique bien à tous les modèles que nous avons traités. En ne conservant que les valeurs élevées du module, il est également possible de détecter les enveloppes (ou frontières) des rouleaux (Figure III-44e); leur topologie est également torique, tout comme les axes. Enfin, nous avons observé que l'évolution du système s'accompagne d'une simplification de l'entremèlement de rouleaux; leur axes tendent à devenir de simples anneaux (les boucles disparaissent), dont le diamètre se réduit jusqu'à l'effondrement de la cellule associée.

**Figure:** Simulations 3D par différences finies du modèle complexe de Ginzburg-Landau. Domaines , $Z_{1}(x, t=0) \approx 0.0$ , $Z_{2}(x, t=0) \approx 0.0$ . Paramètres: $\alpha = 1$ , $\beta = 1$ , $\gamma = 1$ , $\delta = 1.122$ , $K_{r} = 0.40$ . Sauf indications contraires, itérations.
$\begin{figure} \centerline {\begin{tabular}{ccc} \fbox{\epsfxsize=4.5cm \epsfbox... ....90$\ (autre réalisation avec paramètres identiques)} \end{tabular}}\end{figure}$