suivant: 4.5 Modèle complexe de remonter: 4. Simulations macroscopiques par précédent: 4.3 Modèle de Schlögl [Table des matières]
Dans l'introduction à cette partie, les structures de Turing [Turing52] ont déjà
été mentionnées, tant elles représentent le meilleur exemple d'application
de la réaction-diffusion à la simulation de textures réalistes. L'instabilité
de Turing à leur origine détermine une large classe de modèles, qui est
- de très loin - la plus étudiée. Il apparaît que ces modèles ont au moins
deux caractéristiques communes: d'une part, un mécanisme réactionnel à deux
espèces conduisant à une dynamique non-linéaire; et d'autre part, le fait que le
processus de diffusion n'ait pas la même intensité pour les deux espèces.
Lorsque leur coefficients de diffusion sont suffisamment différents, les
réactions chimiques produisent alors des hétérogénéités de concentrations stationnaires.
Les motifs ainsi obtenus présentent en général une grande régularité dans leur
organisation spatiale macroscopique; leur pseudo-périodicité dans l'espace les
caractérise - du moins à une dimension.
Plus précisément, l'une des espèces joue le rôle d' activateur
chimique avec un coefficient de diffusion ![]() ,
tandis que la seconde espèce se comporte comme un inhibiteur de coefficient
de diffusion
,
tandis que la seconde espèce se comporte comme un inhibiteur de coefficient
de diffusion
![]() . L'inhibiteur et l'activateur sont produits
simultanément, par auto-catalyse. Par son action chimique, l'inhibiteur s'oppose
à l'activateur; or celui-ci diffuse plus lentement que l'inhibiteur. Dans son
extension spatiale, il va donc rencontrer des zones déjà atteintes par l'inhibiteur,
où ce dernier est majoritaire. Finalement, il ne pourra franchir de tels obstacles
et restera "confiné" à l'intérieur de régions totalement entourées d'inhibiteur.
Après une phase initiale de formation de ces structures, l'évolution du système
est alors presque arrêtée (il se produit un blocage). Les régions de l'espace
où l'activateur est majoritaire prennent la forme de motifs réguliers, qui sont
considérés comme quasi-stables.
. L'inhibiteur et l'activateur sont produits
simultanément, par auto-catalyse. Par son action chimique, l'inhibiteur s'oppose
à l'activateur; or celui-ci diffuse plus lentement que l'inhibiteur. Dans son
extension spatiale, il va donc rencontrer des zones déjà atteintes par l'inhibiteur,
où ce dernier est majoritaire. Finalement, il ne pourra franchir de tels obstacles
et restera "confiné" à l'intérieur de régions totalement entourées d'inhibiteur.
Après une phase initiale de formation de ces structures, l'évolution du système
est alors presque arrêtée (il se produit un blocage). Les régions de l'espace
où l'activateur est majoritaire prennent la forme de motifs réguliers, qui sont
considérés comme quasi-stables.
En fonction du modèle, mais aussi des valeurs de ses paramètres et des concentrations initiales, les structures (ou motifs) de Turing présentent des géométries variées tels que des rayures plus ou moins sinueuses ou discontinues (lignes brisées), des mosaïques ou pavages de grains arrondis, etc... Chaque type de structure correspond à un domaine de paramètres. A la frontière entre deux domaines, deux types de structures coexistent et entrent en compétition. Bien que les différences entre modèles soient peu importantes, nous présenterons des structures de Turing produites par trois modèles différents. L'un de ces modèles serait peut-être à même de remplacer les deux autres, en générant des motifs identiques. Cependant, il semble que chacun de ces modèles tende préférentiellement à produire un motif distinct, pour des domaines de paramètres étendus.
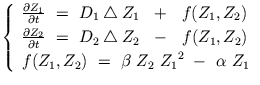 |
(III.-22) |
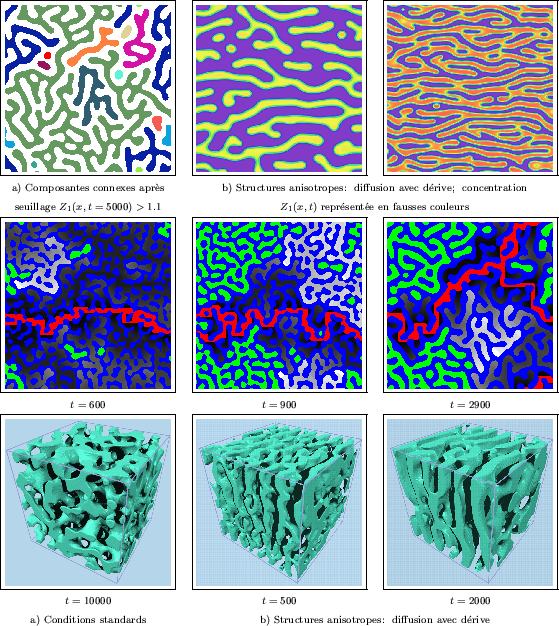
La morphologie des structures de Turing peut être aisément transformée en introduisant
une dérive dans le processus de diffusion. Dans le cas présent, une convolution de l'image
des concentrations par un noyau directionnel permet de réaliser cette dérive.
Des structures plus ou moins anisotropes sont alors
générées, comme sur les deux exemples de la Figure III-18b; il est possible
de fixer précisément le degré d'anisotropie souhaité. Dans une telle situation, les
structures se développent perpendiculairement à la direction de la dérive.
Cette modification du modèle
usuel de réaction-diffusion peut s'avèrer très utile lorsque l'on souhaite reproduire des textures
réelles, qui sont rarement isotropes. Les phénomènes de croissance directionnelle ou encore
d'étirement sont à l'origine de textures anisotropes. C'est par exemple le cas du bois
ou de l'écorce d'un arbre; des matériaux anisotropes se rencontrent aussi fréquemment.
 |
 |
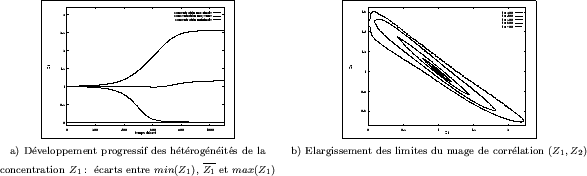
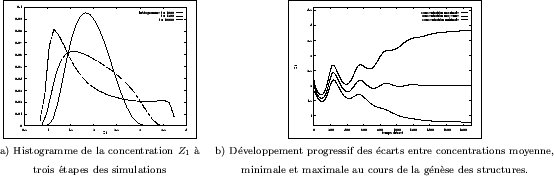
De nombreuses mesures ont été effectuées sur une série de 30 simulations
bidimensionnelles (semblables à celle de la Figure III-17). La Figure III-21a
montre ainsi la cinétique du système. De manière générale, l'évolution globale des concentrations
ne peut fournir aucune information quant au développement d'hétérogénéités. Cependant, il est intéressant
de représenter les concentrations minimales et maximales rencontrées dans le champ de simulation
de
![]() points qui a été utilisé.
La croissance de leur écart par rapport à la concentration moyenne (qui évolue peu) correspond
à la période de formation des structures; par contre, cet indicateur ne peut rendre compte
de leur organisation spatiale.
points qui a été utilisé.
La croissance de leur écart par rapport à la concentration moyenne (qui évolue peu) correspond
à la période de formation des structures; par contre, cet indicateur ne peut rendre compte
de leur organisation spatiale.
Sur la Figure III-21b apparait l'évolution des limites
du nuage de corrélation
![]() . Ce type de diagrammme s'obtient aisément
en représentant par un point tous les couples de concentrations
. Ce type de diagrammme s'obtient aisément
en représentant par un point tous les couples de concentrations
![]() observés dans le système à un instant donné; un nuage de points est alors obtenu.
On trace ensuite son enveloppe, qui détermine
une région à l'intérieur de laquelle toutes les combinaisons
observés dans le système à un instant donné; un nuage de points est alors obtenu.
On trace ensuite son enveloppe, qui détermine
une région à l'intérieur de laquelle toutes les combinaisons
![]() sont possibles
d'un point de vue expérimental, pour un domaine de dimensions fixées. Il s'agit en quelque sorte des contraintes que le modèle
de réaction-diffusion impose au système. Finalement, on analyse l'évolution de ce nuage
de corrélation: un élargissement concentrique peut être constaté, alors que celui-ci prend
une forme ellipsoïdale.
sont possibles
d'un point de vue expérimental, pour un domaine de dimensions fixées. Il s'agit en quelque sorte des contraintes que le modèle
de réaction-diffusion impose au système. Finalement, on analyse l'évolution de ce nuage
de corrélation: un élargissement concentrique peut être constaté, alors que celui-ci prend
une forme ellipsoïdale.
[]
[]
 |
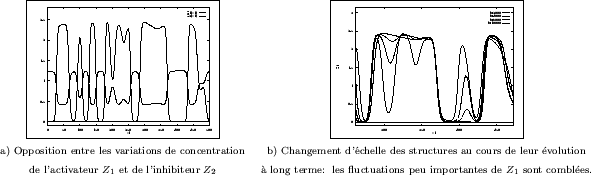
Les profils de concentrations rendent peut-être mieux compte de leur variations spatiales
que les images déjà présentées. Sur la Figure III-22a, l'opposition entre les concentrations
de l'activateur ![]() et de l'inhibiteur
et de l'inhibiteur ![]() s'observe nettement. Les interfaces entre
régions où chaque espèce est ultra-majoritaire, sont de faible épaisseur, et
les gradients de concentrations sont très importants. Ce fait renforce l'idée que le seuillage
des structures ne fait perdre que peu d'information. Le changement d'échelle des structures
peut aussi être constaté sur un profil de concentrations (voir Figure III-22b).
Les fluctuations de concentration s'espacent progressivement, soit en disparaissant dans le
cas de pics étroits, soit en se réunissant en un seul bloc dans le cas de pics rapprochés.
L'analogie avec un filtrage morphologique (de type ouverture-fermeture) n'est pas sans
fondement.
s'observe nettement. Les interfaces entre
régions où chaque espèce est ultra-majoritaire, sont de faible épaisseur, et
les gradients de concentrations sont très importants. Ce fait renforce l'idée que le seuillage
des structures ne fait perdre que peu d'information. Le changement d'échelle des structures
peut aussi être constaté sur un profil de concentrations (voir Figure III-22b).
Les fluctuations de concentration s'espacent progressivement, soit en disparaissant dans le
cas de pics étroits, soit en se réunissant en un seul bloc dans le cas de pics rapprochés.
L'analogie avec un filtrage morphologique (de type ouverture-fermeture) n'est pas sans
fondement.
 |
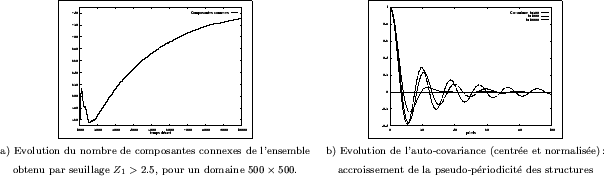
Afin de caractériser la morphologie des structures de Turing, leur auto-covariance a aussi été
mesurée; on pourra la comparer à celle qui a été obtenue pour le modèle de Schlögl.
Sur la Figure III-23a, deux points doivent être soulignés: d'une part, un effet
de "trou" dans la courbe de covariance (valeurs négatives) traduit une répulsion entre structures,
soit une alternance de phase. On confirme ainsi qu'une région où la concentration de l'activateur
est élevée, est obligatoirement entourée d'une région où celle-ci est faible. Cette caractéristique
confère des propriétés particulières aux structures de Turing. On ne vérifie cependant pas une
complète périodicité des structures; dans ce cas, la covariance oscillerait avec une période égale à leur
espacement. Le phénomène de répulsion caractérise bien les structures de Turing, par rapport
à d'autres modèles; son apparition se produit dès la génèse des structures: on comparera les
courbes pour ![]() ,
, ![]() et
et ![]() (dans ce dernier cas, la répulsion a presque atteint
son maximum). D'autre part, on constate également une augmentation de l'échelle des
structures (comparer les courbes pour
(dans ce dernier cas, la répulsion a presque atteint
son maximum). D'autre part, on constate également une augmentation de l'échelle des
structures (comparer les courbes pour ![]() et
et ![]() ), comme pour le modèle
de Schlögl.
), comme pour le modèle
de Schlögl.
 |
La covariance croisée entre les concentrations des deux espèces est donnée par
| (III.-23) |
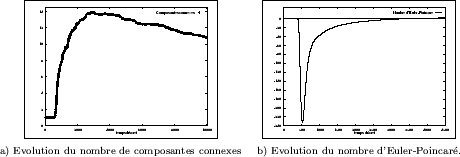
Comme pour le modèle précédent, nous avons aussi mesuré l'évolution du nombre de composantes
connexes et du nombre d'Euler-Poincaré après seuillage (Figure III-24). En deux dimensions, on constate une
inter-connection assez importante des structures, puisque - en moyenne - on
décompte au plus ![]() composantes dans un domaine
composantes dans un domaine
![]() (pour des paramètres
donnés). Ce nombre évolue ensuite très lentement, comme toutes les grandeurs mesurées durant la période qui
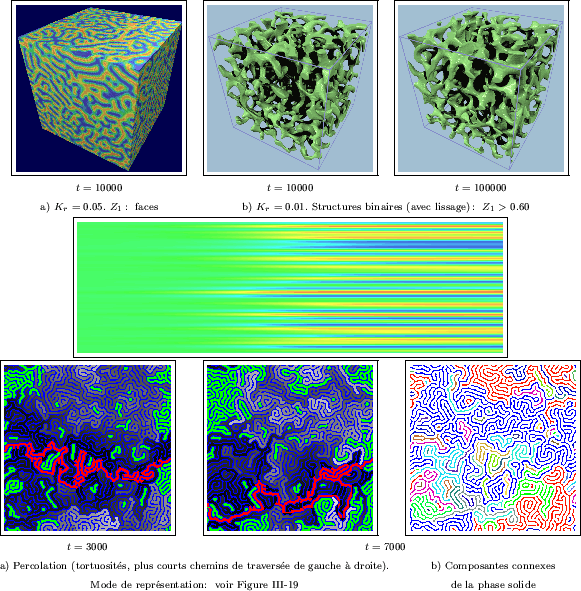
suit la formation initiale des structures. Une carte des composantes
connexes est par ailleurs présentée sur la Figure III-18a, une couleur différente étant
attribuée à chaque composante après son identification. Pour cette réalisation, on constate
que l'une des composantes (en vert clair) couvre plus de la moitié des structures en surface.
Un tel phénomène se reproduit souvent pour d'autres réalisations.
L'imbrication initiale des deux phases conduit à un nombre de "trous" très important, d'où une valeur
négative du nombre d'Euler-Poincaré; ces derniers disparaissent ensuite et le nombre d'Euler-Poincaré tend
de plus en plus lentement vers zéro.
(pour des paramètres
donnés). Ce nombre évolue ensuite très lentement, comme toutes les grandeurs mesurées durant la période qui
suit la formation initiale des structures. Une carte des composantes
connexes est par ailleurs présentée sur la Figure III-18a, une couleur différente étant
attribuée à chaque composante après son identification. Pour cette réalisation, on constate
que l'une des composantes (en vert clair) couvre plus de la moitié des structures en surface.
Un tel phénomène se reproduit souvent pour d'autres réalisations.
L'imbrication initiale des deux phases conduit à un nombre de "trous" très important, d'où une valeur
négative du nombre d'Euler-Poincaré; ces derniers disparaissent ensuite et le nombre d'Euler-Poincaré tend
de plus en plus lentement vers zéro.
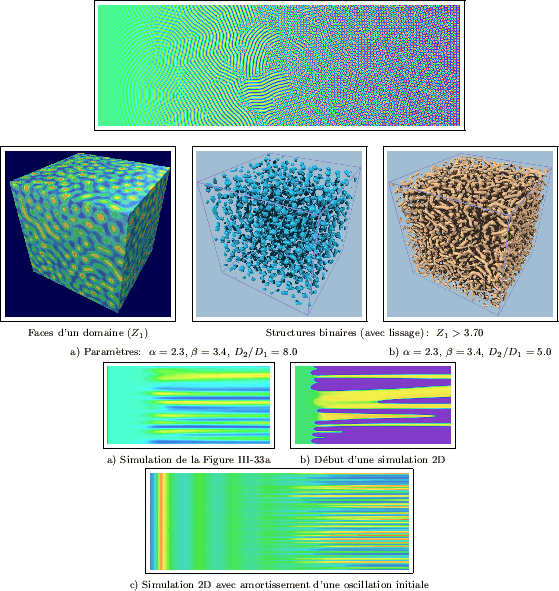
Les modèles de réaction-diffusion peuvent aussi être mis en oeuvre afin d'obtenir des milieux
poreux aléatoires. Une réalisation tri-dimensionnelle de ce modèle est ainsi présentée
sur la Figure III-20a, après seuillage (et lissage) des structures.
Nous avons constaté que la morphologie de ces structures de Turing est comparable à deux et
trois dimensions. Cependant, toutes les réalisations qui ont été produites vérifient
une propriété tout à fait remarquable: après binarisation, les deux phases sont
totalement interconnectées, ce qui ne s'observe jamais à deux dimensions.
On détecte ainsi une seule composante connexe aussi
bien pour la partie "solide" que pour son complémentaire (le vide), compte tenu
des conditions aux limites périodiques. Comme en deux
dimensions, nous avons par ailleurs produit des structures anisotropes (voir
Figure III-20b). L'imbrication des structures est réduite
lorsqu'elles s'organisent préférentiellement dans une direction de l'espace.
 |
En présence de morphologies aussi complexes, il nous a semblé intéressant d'effectuer
des propagations géodésiques (voir par exemple [Tovena98,Decker98a])
à travers le milieu poreux virtuel constitué par
les structures de Turing après leur binarisation. Considérons qu'un fluide circule
exclusivement dans les pores du milieu, alors que son bord gauche constitue la face (ou arête)
d'entrée, et son bord droit, la face de sortie. Un test de percolation
consiste à chercher l'existence d'au moins un passage (ou chemin géodésique) entre les deux faces,
à travers les pores uniquement. Le cas échéant, on détecte alors l'ensemble des pores
qui percolent (ou pores "ouverts") : ils sont aussi bien accessibles par un chemin issu de la face d'entrée que de
la face de sortie. Les pores restants sont dits "non-traversés" ou encore "fermés". On détermine également
la tortuosité en tout point du milieu qui fait partie d'un pore ouvert :
Définition: La tortuosité locale en un point ![]() correspond à la longueur du plus court
chemin géodésique qui passe par
correspond à la longueur du plus court
chemin géodésique qui passe par ![]() en reliant la face d'entrée à la face de sortie à travers les pores,
divisée par la distance euclidienne
en reliant la face d'entrée à la face de sortie à travers les pores,
divisée par la distance euclidienne ![]() entre les deux faces.
entre les deux faces.
En conséquence, la tortuosité locale est égale à ![]() en tout point d'un chemin direct (en ligne droite)
entre les deux faces. De plus, il est possible de déterminer la distribution des tortuosités
pour toute la porosité ouverte; cette mesure constitue une caractérisation morphologique des
structures étudiées. La valeur minimale de la tortuosité est attribuée à tous les points qui
se trouvent sur le plus court chemin géodésique entre les deux faces. Au contraire, la tortuosité
est la plus élevée aux points (isolés, en général) qui sont les plus éloignés des deux faces,
tout en restant accessibles.
en tout point d'un chemin direct (en ligne droite)
entre les deux faces. De plus, il est possible de déterminer la distribution des tortuosités
pour toute la porosité ouverte; cette mesure constitue une caractérisation morphologique des
structures étudiées. La valeur minimale de la tortuosité est attribuée à tous les points qui
se trouvent sur le plus court chemin géodésique entre les deux faces. Au contraire, la tortuosité
est la plus élevée aux points (isolés, en général) qui sont les plus éloignés des deux faces,
tout en restant accessibles.
Comme la recherche de composantes connexes, la mesure de la tortuosité repose sur des
algorithmes élémentaires issus de la théorie des graphes (la trame de l'image constituant
un graphe régulier). La recherche d'un plus court chemin entre deux points (ou sommets) est effectuée
au moyen d'une file d'attente de points de passage intermédiaires. Cette file d'attente donne la garantie
que les points en attente dans la file sont rangés dans l'ordre des distances croissantes par rapport au point
de départ : un parcours "en largeur" du graphe est effectué. Il est ainsi immédiat d'introduire un ensemble de points de départ dans la file
- en l'occurrence, tous les points du bord gauche du milieu. Pour chaque point extrait de la file,
ses voisins appartenant aux pores y sont insérés (en queue).
Dans le cas d'une image, cet algorithme réalise des propagations selon une trame donnée; dans son
implantation actuelle, il n'utilise donc pas de distances euclidiennes. En trame carrée, il
présente l'un des deux inconvénients suivants : si l'on se déplace en 4-connexité (à deux dimensions), les déplacements
prennent l'aspect de "marches d'escalier" peu naturelles; en 8-connexité, les directions de déplacement
sont plus nombreuses, mais les déplacements "en diagonale" comptent pour une distance unitaire aussi bien
que les déplacements selon les directions principales. Nous avons retenu cette seconde possibilité; en
trame cubique, les déplacements sont effectués en 26-connexité. La tortuosité est calculée en deux étapes
[Demarty96] : une première propagation permet de calculer les plus courts chemins (distances ![]() ) de la face
d'entrée à tout point (accessible) du milieu. Une seconde propagation fournit la même information
à partir de la face de sortie (distances
) de la face
d'entrée à tout point (accessible) du milieu. Une seconde propagation fournit la même information
à partir de la face de sortie (distances ![]() ). La combinaison des deux valeurs
permet de connaître quels sont les pores qui percolent, et leur tortuosité éventuelle
soit
). La combinaison des deux valeurs
permet de connaître quels sont les pores qui percolent, et leur tortuosité éventuelle
soit
![]() .
.
Un exemple de percolation au travers de structures de Turing est présenté sur la Figure III-19.
La mesure est effectuée alors que les structures se développent, et rendent ainsi de plus
en plus difficile le passage d'un bord à l'autre. Pour cette réalisation, il n'y a ainsi plus
percolation pour ![]() , un rétrécissement critique se refermant complètement. L'algorithme
appliqué permet de détecter automatiquement les passages les plus courts entre les deux faces (représentés
en rouge), c'est à dire la solution du labyrinthe. Pour les structures étudiées,
il devient difficile de trouver visuellement cette solution (du moins, en peu de temps), compte tenu
de leur tortuosité importante. Il s'agit aussi d'une caractéristique commune à la majorité des
structures de Turing, et à notre connaissance de telles mesures n'ont jamais été effectuée pour ces modèles.
, un rétrécissement critique se refermant complètement. L'algorithme
appliqué permet de détecter automatiquement les passages les plus courts entre les deux faces (représentés
en rouge), c'est à dire la solution du labyrinthe. Pour les structures étudiées,
il devient difficile de trouver visuellement cette solution (du moins, en peu de temps), compte tenu
de leur tortuosité importante. Il s'agit aussi d'une caractéristique commune à la majorité des
structures de Turing, et à notre connaissance de telles mesures n'ont jamais été effectuée pour ces modèles.
Les histogrammes des tortuosités locales correspondants aux propagations géodésiques sont donnés
sur la Figure III-25a : il se confirme que la tortuosité augmente durant
la formation des structures.
Sur 30 réalisations cependant, environ la moitié d'entre-elles cessent ainsi de percoler après un
certain temps, assez court en général; dans l'intervalle, leur tortuosité augmente.
Pour toutes les autres réalisations, la tortuosité baisse à long terme alors
que la complexité des structures diminue en relation avec l'augmentation de leur
taille. En trois dimensions, la situation est très différente puisque les pores sont entièrement
interconnectés. Il a ainsi été observé que toutes les réalisations obtenues percolent. En conséquence,
la tortuosité des structures diminue à long terme (avec leur changement d'échelle), comme
le montre la Figure III-25b; un resserrement de la distribution des tortuosités locales
apparait nettement.
Enfin, la méthode des marcheurs aléatoires décrite au chapitre II-2.2 a été appliquée afin d'estimer la diffusion au travers d'un milieu poreux représenté par une structure de Turing tri-dimensionnelle après binarisation. Les variogrammes moyens des trajectoires d'un grand nombre de marcheurs aléatoires sont présentés sur la Figure III-26a, à quatre étapes différentes de l'évolution d'une réalisation. Si l'on suppose que la loi de Fick est vérifiée dans un tel milieu, le coefficient de diffusion d'un milieu homogène équivalent montre une faible augmentation au cours du temps, en passant de
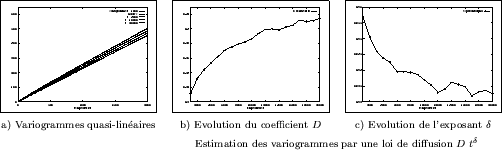 |
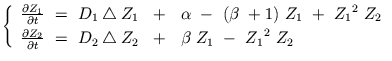 |
(III.-24) |
Des motifs très réguliers peuvent être obtenus à partir de ce modèle.
En deux dimensions, il s'agit: d'une part de disques disposés dans l'espace
selon des arrangements (ou pavages) hexagonaux; et d'autre part, de bandes ou rayures
régulièrement espacées. Nous nous intéresserons plus particulièrement au
cas des disques, que l'on observera sur les deux réalisations de la Figure III-27.
Comme pour le modèle symétrique, les variations des concentrations de l'activateur (![]() )
et de l'inhibiteur (
)
et de l'inhibiteur (![]() ) sont en opposition (comparer les deux images de gauche).
Cependant, les structures obtenues ne sont manifestement plus auto-duales. Après seuillage
des concentrations élevées (du jaune au rouge), l'image
) sont en opposition (comparer les deux images de gauche).
Cependant, les structures obtenues ne sont manifestement plus auto-duales. Après seuillage
des concentrations élevées (du jaune au rouge), l'image ![]() serait fort semblable
à un ensemble aléatoire de disques placés en tenant compte d'une distance de répulsion
importante - précisément, un modèle de type hard-core (voir chapitre I-1) -,
jusqu'à "saturation" du milieu.
serait fort semblable
à un ensemble aléatoire de disques placés en tenant compte d'une distance de répulsion
importante - précisément, un modèle de type hard-core (voir chapitre I-1) -,
jusqu'à "saturation" du milieu.
Une étude attentive de l'image des concentrations de l'activateur (![]() ) sur la Figure III-27
permet de constater que l'arrangement hexagonal des grains est loin d'être parfait.
Il présente de nombreux défauts ou décalages: si une majorité de grains dispose de
) sur la Figure III-27
permet de constater que l'arrangement hexagonal des grains est loin d'être parfait.
Il présente de nombreux défauts ou décalages: si une majorité de grains dispose de ![]() voisins,
certains en ont
voisins,
certains en ont ![]() , et d'autres
, et d'autres ![]() uniquement. Nous avons souhaité quantifier ces
défauts, suivre leur évolution et analyser leur répartition dans l'espace.
uniquement. Nous avons souhaité quantifier ces
défauts, suivre leur évolution et analyser leur répartition dans l'espace.
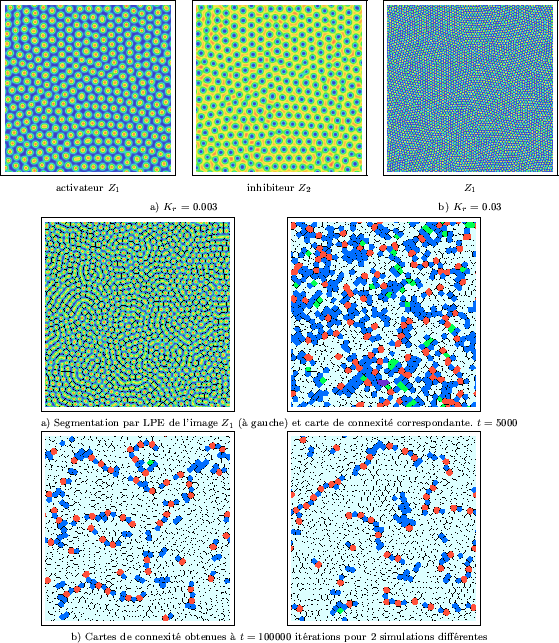 |
La première étape consiste à segmenter l'image des concentrations, afin
de localiser avec exactitude les frontières entre les grains. Il est alors
possible de les identifier, en leur attribuant des labels (ou numéros) distincts.
Dans ce but, nous avons fait appel à l'algorithme de la ligne de partage des eaux (LPE)
[Meyer90b,Meyer92], déjà
appliqué pour déterminer les frontières entre polyèdres de Voronoï (chapitre I-2.2).
Pour rappel, l'image à segmenter est considérée comme un relief formé de bassins
versants isolés, que l'on souhaite délimiter. Dans sa version initiale, ce
traitement associe un bassin (une région) à tout minima local de l'image. Il
est souvent préférable de définir à l'avance les positions approximatives
des bassins au moyen de marqueurs. En fonction du relief, l'algorithme permet
alors de déterminer la position précise des frontières entre bassins, soient
les lignes de partage des eaux. Dans le cas présent, l'image ![]() est inversée
afin que le centre de chaque grain corresponde à un minimum local. De plus, pour obtenir
un marqueur unique par grain, cette image est seuillée à un niveau très bas : on
obtient alors une image binaire des centres des grains. L'utilisation de ces
marqueurs permet de contourner le problème posé par l'existence
de plusieurs minima locaux au centre de certains grains. Finalement, les grains
sont segmentés, comme sur la partie gauche de la Figure III-28a où les frontières ont été
superposées (en noir) à l'image de la concentration
est inversée
afin que le centre de chaque grain corresponde à un minimum local. De plus, pour obtenir
un marqueur unique par grain, cette image est seuillée à un niveau très bas : on
obtient alors une image binaire des centres des grains. L'utilisation de ces
marqueurs permet de contourner le problème posé par l'existence
de plusieurs minima locaux au centre de certains grains. Finalement, les grains
sont segmentés, comme sur la partie gauche de la Figure III-28a où les frontières ont été
superposées (en noir) à l'image de la concentration ![]() .
.
La mesure de la connexité des grains constitue la seconde étape.
Pour toute région, il s'agit simplement de compter le nombre de régions
voisines en parcourant sa frontière. Par convention, deux
régions seront voisines si leur frontière commune comporte plus de ![]() pixels
(nous avons choisi
pixels
(nous avons choisi ![]() ). Il en résulte qu'une carte des connexités
peut être établie, en attribuant une couleur à chaque région en fonction
de son nombre de voisins. La carte correspondant à l'image segmentée
est présentée sur la partie droite de la Figure III-28a. Après seulement
). Il en résulte qu'une carte des connexités
peut être établie, en attribuant une couleur à chaque région en fonction
de son nombre de voisins. La carte correspondant à l'image segmentée
est présentée sur la partie droite de la Figure III-28a. Après seulement
![]() itérations, le nombre d'hexagones (en blanc) est encore assez
faible (
itérations, le nombre d'hexagones (en blanc) est encore assez
faible (![]() ). Les grains se déplacent très lentement, mais ils tendent à
construire un réseau hexagonal parfait; dans ce contexte,
toutes les régions non-hexagonales seront considérées comme des défauts.
Sur la Figure III-28b, nous étudions
les cartes de connexité obtenues après
). Les grains se déplacent très lentement, mais ils tendent à
construire un réseau hexagonal parfait; dans ce contexte,
toutes les régions non-hexagonales seront considérées comme des défauts.
Sur la Figure III-28b, nous étudions
les cartes de connexité obtenues après ![]() itérations pour deux
réalisations différentes, à partir de paramètres identiques. D'une part, les
régions se sont transformées en hexagones dans leur très grande majorité (plus de
itérations pour deux
réalisations différentes, à partir de paramètres identiques. D'une part, les
régions se sont transformées en hexagones dans leur très grande majorité (plus de ![]() ).
D'autre part, il est surprenant de constater que les défauts résiduels forment
des lignes discontinues, qui divisent grossièrement le milieu en zones
homogènes étendues qui sont exemptes de défauts. Ces lignes semblent ainsi
jouer le rôle de joints de grains macroscopiques - où chaque grain
macroscopique correspond à un ensemble connexe d'hexagones.De plus, les lignes
de défauts sont constituées d'une alternance de pentagones (connexité 5) et
d'heptagones (connexité 7). Dans un tout autre contexte, un mode d'organisation
très similaire a été observé au cours de simulations de structures cellulaires produites
par solidification directionnelle [Kassner98]. Par ailleurs,
on observera aussi quelques plans de glissement constitués essentiellement de regroupements
de pentagones (en bleu); ces derniers présentent un alignement de frontières.
Alors que la plupart des grains microscopiques se bloquent mutuellement (c'est en particulier
le cas des hexagones), de telles lignes droites doivent favoriser leur déplacement,
ou même le glissement entier d'une zone par rapport à une autre. Les distributions
moyennes des connexités des grains ont été estimées sur
).
D'autre part, il est surprenant de constater que les défauts résiduels forment
des lignes discontinues, qui divisent grossièrement le milieu en zones
homogènes étendues qui sont exemptes de défauts. Ces lignes semblent ainsi
jouer le rôle de joints de grains macroscopiques - où chaque grain
macroscopique correspond à un ensemble connexe d'hexagones.De plus, les lignes
de défauts sont constituées d'une alternance de pentagones (connexité 5) et
d'heptagones (connexité 7). Dans un tout autre contexte, un mode d'organisation
très similaire a été observé au cours de simulations de structures cellulaires produites
par solidification directionnelle [Kassner98]. Par ailleurs,
on observera aussi quelques plans de glissement constitués essentiellement de regroupements
de pentagones (en bleu); ces derniers présentent un alignement de frontières.
Alors que la plupart des grains microscopiques se bloquent mutuellement (c'est en particulier
le cas des hexagones), de telles lignes droites doivent favoriser leur déplacement,
ou même le glissement entier d'une zone par rapport à une autre. Les distributions
moyennes des connexités des grains ont été estimées sur ![]() réalisations,
après
réalisations,
après ![]() et
et ![]() itérations. Sur la Figure III-29, on pourra ainsi vérifier
l'augmentation du nombre de régions 6-connexes au détriment des autres connexités.
itérations. Sur la Figure III-29, on pourra ainsi vérifier
l'augmentation du nombre de régions 6-connexes au détriment des autres connexités.
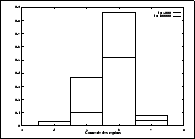 |
Pour ces ![]() réalisations, d'autres mesures plus habituelles ont
été effectuées. Sur la Figure III-30a, l' histogramme des concentrations
de l'activateur est de type gaussien vers le début des simulations (
réalisations, d'autres mesures plus habituelles ont
été effectuées. Sur la Figure III-30a, l' histogramme des concentrations
de l'activateur est de type gaussien vers le début des simulations (![]() ).
Il change ensuite complètement d'aspect avec le développement des structures. Comme
pour le modèle précédent, on observera aussi la croissance de l'écart entre les
concentrations minimale, maximale et moyenne sur la Figure III-30b; elle s'accompagne
de l'amortissement d'une oscillation initiale. Le nombre de composantes
connexes obtenues après seuillage des grains est bien sûr très élevé pour
ce type de structures (Figure III-31a). Son augmentation est due à la
division de certains grains "doubles", qui sont ainsi éliminés en raison
de leur taille trop importante pour leur permettre d'entrer dans l'assemblage "parfait"
que le système construit progressivement. Enfin, l'auto-covariance du modèle
se présente sous la forme d'une sinusoïde dont l'amplitude diminue
exponentiellement (Figure III-31b). Un tel comportement traduit la pseudo-périodicité
des structures générées par le Brusselator; on observe son renforcement
au cours du temps (comparer les courbes pour
).
Il change ensuite complètement d'aspect avec le développement des structures. Comme
pour le modèle précédent, on observera aussi la croissance de l'écart entre les
concentrations minimale, maximale et moyenne sur la Figure III-30b; elle s'accompagne
de l'amortissement d'une oscillation initiale. Le nombre de composantes
connexes obtenues après seuillage des grains est bien sûr très élevé pour
ce type de structures (Figure III-31a). Son augmentation est due à la
division de certains grains "doubles", qui sont ainsi éliminés en raison
de leur taille trop importante pour leur permettre d'entrer dans l'assemblage "parfait"
que le système construit progressivement. Enfin, l'auto-covariance du modèle
se présente sous la forme d'une sinusoïde dont l'amplitude diminue
exponentiellement (Figure III-31b). Un tel comportement traduit la pseudo-périodicité
des structures générées par le Brusselator; on observe son renforcement
au cours du temps (comparer les courbes pour ![]() et
et ![]() itérations).
itérations).
 |
 |
Il a été mentionné que le Brusselator peut également être à l'origine d'autres structures
qui prennent la forme de rayures. Le paramètre de contrôle ![]() participe notamment
à la sélection du type de structures générées. Pour connaître l'influence d'un
paramètre quelconque
participe notamment
à la sélection du type de structures générées. Pour connaître l'influence d'un
paramètre quelconque ![]() sur la morphologie d'un modèle, il est possible de réaliser des séries
de simulations, avec par exemple un accroissement régulier de la valeur de
sur la morphologie d'un modèle, il est possible de réaliser des séries
de simulations, avec par exemple un accroissement régulier de la valeur de ![]() .
Une solution plus ingénieuse consiste à régionaliser ce paramètre dans
un même domaine de simulation; les travaux de Borckmans et al. comptent
parmi les premiers à la mettre en oeuvre [Borckmans92]. Pour le paramètre
étudié, une rampe linéaire (ou gradient) est ainsi établie selon l'une
des directions principales (x ou y), soit par exemple
.
Une solution plus ingénieuse consiste à régionaliser ce paramètre dans
un même domaine de simulation; les travaux de Borckmans et al. comptent
parmi les premiers à la mettre en oeuvre [Borckmans92]. Pour le paramètre
étudié, une rampe linéaire (ou gradient) est ainsi établie selon l'une
des directions principales (x ou y), soit par exemple
![]() .
Au cours de la simulation, les structures
se développent alors différemment selon leur position
.
Au cours de la simulation, les structures
se développent alors différemment selon leur position ![]() dans le domaine: une unique simulation permet
d'explorer un large spectre de valeurs. Mais plus
encore, l'intérêt d'une telle approche réside dans la continuité des structures
obtenues. Les zones de transition entre deux morphologies bien distinctes présentent
souvent le maximum d'interêt; on observe parfois l'existence éphémère d'une troisième
morphologie à la frontière des deux autres. Le manque de sensibilité constitue le
principal inconvénient pour cette méthode: si le gradient du paramètre
dans le domaine: une unique simulation permet
d'explorer un large spectre de valeurs. Mais plus
encore, l'intérêt d'une telle approche réside dans la continuité des structures
obtenues. Les zones de transition entre deux morphologies bien distinctes présentent
souvent le maximum d'interêt; on observe parfois l'existence éphémère d'une troisième
morphologie à la frontière des deux autres. Le manque de sensibilité constitue le
principal inconvénient pour cette méthode: si le gradient du paramètre ![]() est
trop fort, certains comportements (ou modes) intermédiaires ne seront pas observables.
Une contamination des morphologies a aussi été constatée : certaines structures se propagent
dans la direction du gradient - en particulier lorsqu'il est trop faible.
Les régions où ces structures se retrouvent correspondent alors à des valeurs de
est
trop fort, certains comportements (ou modes) intermédiaires ne seront pas observables.
Une contamination des morphologies a aussi été constatée : certaines structures se propagent
dans la direction du gradient - en particulier lorsqu'il est trop faible.
Les régions où ces structures se retrouvent correspondent alors à des valeurs de ![]() pour
lesquelles elles ne seraient pas apparues dans une simulation classique (avec une valeur unique
de
pour
lesquelles elles ne seraient pas apparues dans une simulation classique (avec une valeur unique
de ![]() pour tout le domaine).
pour tout le domaine).
Nous avons appliqué la méthode de la rampe linéaire au paramètre ![]() .
La Figure III-32 en présente les résultats: pour
.
La Figure III-32 en présente les résultats: pour ![]() , la partie droite du domaine est
constituée d'un assemblage hexagonal de disques, tel que nous l'avons déjà étudié.
La partie restante du domaine a permis l'établissement de structures totalement différentes:
des bandes (ou rayures) à l'espacement régulier. Des ensembles de disques peu apparents
sont observables épisodiquement au niveau des zones de dislocations (ou de raccords)
des bandes. A l'intérieur de ces deux régions distinctes, la morphologie des
structures est sensiblement homogène. Dans la partie la plus à gauche du domaine, les bandes montrent cependant
une plus grande continuité, ainsi que des courbures plus harmonieuses. Du coté droit,
les disques sont plus contrastés et leur limites plus précises pour des valeurs
supérieures de
, la partie droite du domaine est
constituée d'un assemblage hexagonal de disques, tel que nous l'avons déjà étudié.
La partie restante du domaine a permis l'établissement de structures totalement différentes:
des bandes (ou rayures) à l'espacement régulier. Des ensembles de disques peu apparents
sont observables épisodiquement au niveau des zones de dislocations (ou de raccords)
des bandes. A l'intérieur de ces deux régions distinctes, la morphologie des
structures est sensiblement homogène. Dans la partie la plus à gauche du domaine, les bandes montrent cependant
une plus grande continuité, ainsi que des courbures plus harmonieuses. Du coté droit,
les disques sont plus contrastés et leur limites plus précises pour des valeurs
supérieures de ![]() . Enfin, à la frontière entre les deux types de morphologies,
des sous-domaines homogènes - formés de bandes ou de disques - s'organisent à une
échelle plus grande : des structures aléatoires hiérarchiques (à deux échelles) sont
ainsi obtenues. Cette frontière imprécise correspond à une valeur critique de
. Enfin, à la frontière entre les deux types de morphologies,
des sous-domaines homogènes - formés de bandes ou de disques - s'organisent à une
échelle plus grande : des structures aléatoires hiérarchiques (à deux échelles) sont
ainsi obtenues. Cette frontière imprécise correspond à une valeur critique de ![]() ,
les autres paramètres du modèle (
,
les autres paramètres du modèle (![]() et
et
![]() ) étant fixés.
) étant fixés.
 |
En dimension trois, les disques produits par le Brusselator deviennent autant de grains
approximativement sphériques, comme sur la Figure III-33 (image au centre). D'autres
structures plus allongées peuvent aussi être obtenues (image de droite). Dans ces deux
cas, le nombre de composantes connexes reste très élevé. La tortuosité de telles
structures de Turing est faible en comparaison avec le modèle précédent.
La stabilité des structures peut s'observer nettement sur les profils spatio-temporels de la Figure III-34 : les lignes horizontales y traduisent la persistence temporelle des hétérogénéités de concentations. Au contraire, les bandes verticales présentes au début du tracé (à gauche) sur la Figure III-34c correspondent à des oscillations temporelles homogènes, où tous les points du système sont en phase. Pour ce modèle, l'étape de formation des structures représente la partie la plus intéressante d'un tracé spatio-temporel (voir Figure III-34b). Dans certaines conditions, on assiste en effet à une compétition entre différents grains: une partie d'entre-eux disparaissent - du moins du profil mesuré (ils peuvent aussi s'être déplacés dans le domaine). Une série de pics de longueurs inégales sont ainsi observables sur ce tracé.
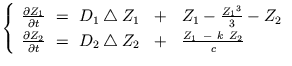 |
(III.-25) |
Au début de leur formation, les textures produites par ce modèle ressemblent
quelque peu aux motifs granulaires obtenus avec le Brusselator (Figure III-35, image de gauche).
Elles s'en différencient ensuite, lorsque les grains isolés fusionnent pour donner
naissance à des branches qui sont connectées en un réseau très ramifié (image de droite).
Après binarisation, les structures résultantes ont alors toutes les caractéristiques d'un labyrinthe aléatoire;
les "chemins" qui les traversent présentent de nombreux embranchements.
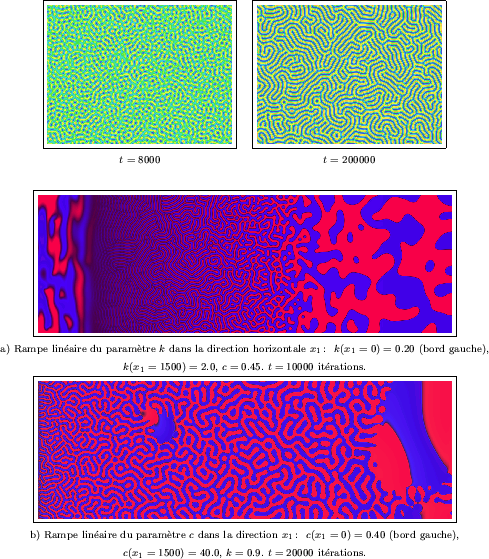 |
Afin d'explorer le rôle des paramètres ![]() et
et ![]() , des simulations avec rampes
linéaires ont été réalisées, comme dans le cas du Brusselator. La Figure III-36a
regroupe une grande variété de comportements, tandis que la valeur de
, des simulations avec rampes
linéaires ont été réalisées, comme dans le cas du Brusselator. La Figure III-36a
regroupe une grande variété de comportements, tandis que la valeur de ![]() augmente régulièrement de gauche à droite. A l'extrême gauche du domaine,
une première région se distingue: elle renferme des structures aux contours flous,
qui sont instables et oscillent en permanence; il ne s'agit pas de structures de Turing.
Plus à droite apparaît le labyrinthe qui nous intéresse. Sa morphologie change
graduellement: on observe d'abord de simples rayures quasi rectilignes (
augmente régulièrement de gauche à droite. A l'extrême gauche du domaine,
une première région se distingue: elle renferme des structures aux contours flous,
qui sont instables et oscillent en permanence; il ne s'agit pas de structures de Turing.
Plus à droite apparaît le labyrinthe qui nous intéresse. Sa morphologie change
graduellement: on observe d'abord de simples rayures quasi rectilignes (![]() ), puis l'angle et la
fréquence de leurs changements de direction augmentent; le labyrinthe devient alors
de plus en plus ramifié.
Peu après le tiers du domaine (à partir de la gauche),
un maximum de tortuosité semble atteint (
), puis l'angle et la
fréquence de leurs changements de direction augmentent; le labyrinthe devient alors
de plus en plus ramifié.
Peu après le tiers du domaine (à partir de la gauche),
un maximum de tortuosité semble atteint (![]() ), avant que les discontinuités n'augmentent
et ne transforment le labyrinthe en un amas de branches déconnectées (
), avant que les discontinuités n'augmentent
et ne transforment le labyrinthe en un amas de branches déconnectées (![]() ).
Enfin, cette dégénérescence s'achève dans la partie droite du domaine (
).
Enfin, cette dégénérescence s'achève dans la partie droite du domaine (![]() ) par
des structures arrondies beaucoup plus grandes, qui sont similaires à celles
que nous avons déjà produites grâce au modèle de Walgraef. La rampe linéaire du
paramètre
) par
des structures arrondies beaucoup plus grandes, qui sont similaires à celles
que nous avons déjà produites grâce au modèle de Walgraef. La rampe linéaire du
paramètre ![]() présente moins d'intérêt. De gauche à droite sur la Figure III-36b,
les structures changent lentement d'échelle de taille, mais leur morphologie ne
semble pas évoluer. En fait, les différences observées concernent davantage la dynamique
des structures: leur instabilité et leur mobilité augmentent avec la valeur de
présente moins d'intérêt. De gauche à droite sur la Figure III-36b,
les structures changent lentement d'échelle de taille, mais leur morphologie ne
semble pas évoluer. En fait, les différences observées concernent davantage la dynamique
des structures: leur instabilité et leur mobilité augmentent avec la valeur de ![]() .
C'est ainsi qu'apparaissent des lacunes (ou "trous") oscillantes au sein du labyrinthe;
elles sont tout d'abord rares (un seul cas sur la réalisation présentée),
puis finissent par envahir tout le milieu, au voisinage du bord droit (
.
C'est ainsi qu'apparaissent des lacunes (ou "trous") oscillantes au sein du labyrinthe;
elles sont tout d'abord rares (un seul cas sur la réalisation présentée),
puis finissent par envahir tout le milieu, au voisinage du bord droit (![]() ).
).
Des structures tout aussi complexes sont obtenues à trois dimensions
(Figure III-37). Après binarisation, elles prennent l'aspect d'un réseau d'autant plus
ramifié qu'il dispose d'un degré de liberté supplémentaire pour
se développer. De chaque noeud de réseau partent de nombreuses branches, dans diverses
directions; en deux dimensions, ces embranchements ne comportent en général que trois branches
(en forme de "Y"). Ce type de milieu évoque par exemple une mousse de polymères très poreuse, ou
encore certains tissus de cellules en biologie.
[]
[]
Un profil spatio-temporel du modèle de Maginu est présenté sur la Figure III-38.
Il est difficile de le différencier des profils obtenus dans le cas du Brusselator:
les bandes se traduisent également par des lignes horizontales, dont la largeur
varie cependant en fonction de l'angle avec lequel elles intersectent le profil mesuré.
Les labyrinthes constituent par contre des structures du plus grand intérêt pour
effectuer des propagations géodésiques. Il est certain que les chemins de traversée
de ces labyrinthes sont difficiles à détecter manuellement. Les tortuosités sont encore
plus élevées que dans le cas du modèle de Walgraef. Sur la Figure III-39a, on observera
la complication des plus courts chemins (en rouge) qui donnent "la solution optimale
du labyrinthe", dont la tortuosité atteint ![]() fois la distance entre bords.
Une grande partie du milieu est accessible (percole) et renferme
autant de détours possibles - les seules parties fermées sont colorées en vert.
Les chemins du bord gauche au bord droit qui passent par une région colorée
en gris clair, comptent parmi les plus détournés - il s'agit en quelque sorte, d'un
indicateur de "fausse route". Enfin, l'interconnexion des parois du labyrinthe est
élevée (pour
fois la distance entre bords.
Une grande partie du milieu est accessible (percole) et renferme
autant de détours possibles - les seules parties fermées sont colorées en vert.
Les chemins du bord gauche au bord droit qui passent par une région colorée
en gris clair, comptent parmi les plus détournés - il s'agit en quelque sorte, d'un
indicateur de "fausse route". Enfin, l'interconnexion des parois du labyrinthe est
élevée (pour ![]() ), comme le montre une carte des composantes connexes sur
la Figure III-39b. Il est étonnant que les différentes composantes (colorées
distinctement) induisent un partage du milieu à une échelle bien plus grande que
celle des structures. Si l'on trace leurs enveloppes connexes respectives, on obtient alors
un modèle intéressant de partition aléatoire macroscopique.
), comme le montre une carte des composantes connexes sur
la Figure III-39b. Il est étonnant que les différentes composantes (colorées
distinctement) induisent un partage du milieu à une échelle bien plus grande que
celle des structures. Si l'on trace leurs enveloppes connexes respectives, on obtient alors
un modèle intéressant de partition aléatoire macroscopique.
 |
 Decker, Luc. "Modèles de structures aléatoires de type réaction-diffusion". PhD diss. (191 p.), Paris, ENSMP-CMM, 1999.
Decker, Luc. "Modèles de structures aléatoires de type réaction-diffusion". PhD diss. (191 p.), Paris, ENSMP-CMM, 1999.