Modèles de Structures Aléatoires de Type Réaction-Diffusion - Thèse de Morphologie Mathématique - Luc Decker, Ecole des Mines de Paris (1999)

suivant: 4.4 Instabilité de Turing   remonter: 4. Simulations macroscopiques par   précédent: 4.2 Visualisations   [Table des matières]

4.3 Modèle de Schlögl

Comme premier exemple, reprenons le modèle de Schlögl déjà introduit (section III-3.3). Pour rappel, il s'agit d'un mécanisme de réaction auto-catalytique dans lequel une seule espèce est étudiée. Du point de vue numérique, sa concentration est précisément régie par l'équation de réaction-diffusion suivante:

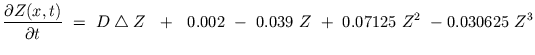$$\frac{\partial Z(x,t)}{\partial t} \ = \ D \bigtriangleup Z \ \ + \ \ 0.002 \ - \ 0.039 \ Z \ + \ 0.07125 \ Z^{2} \ - 0.030625 \ Z^{3}$$ (III.-17)

selon les paramètres donnés dans la référence [Dab89].

Simulations
Les simulations de ce modèle par différences finies sont à l'origine de structures aléatoires dont la morphologie est très proche de celles qui ont déjà été obtenues dans un Gaz sur Réseau avec réactions. Dans le cas de la réalisation présentée sur la Figure III-13a, les conditions initiales correspondent à la concentration d'équilibre instable $Z = 0.7556$, perturbée par un bruit blanc. La séparation du système en régions de concentrations homogènes s'observe très rapidement ($t = 40$ itérations). La répartition spatiale des deux phases évolue ensuite plus lentement; ses hétérogénéités montrent un changement d'échelle progressif. Lorsque des structures sont suffisamment proches, on assiste à leur fusion ou coalescence; par un mécanisme semblable, leur concavités initiales peuvent être comblées. De nombreux grains parfaitement convexes - ou même sphériques - sont ainsi observables. En parallèle, les grains qui n'atteignent pas une taille suffisante sont condamnés à disparaître, au cours d'une lente érosion (ou dissolution), qui est totalement isotrope - à moins que d'autres grains suffisamment proches ne l'influencent. Ce processus semble s'accélèrer exponentiellement avec la diminution de la taille d'un grain. Il est important de noter la dualité de tous ces phénomènes, qui sont observables indifféremment pour les deux phases, leur rôles pouvant être échangés. L'évolution du système peut aussi être analysée grâce au tracé spatio-temporel d'une section du milieu (Figure III-13b); vers son centre, on observera par exemple la disparition d'un grain, dont le profil spatio-temporel ressemble à une parabole (son épaisseur décroît de plus en plus rapidement). En comparaison avec un Gaz sur Réseau, l'absence de bruit résiduel constitue l'un des principaux avantages de ce type d'implantation: les contours des structures apparaissent avec un meilleur constraste; en revanche, l'effet des fluctuations est perdu.

Figure: Simulation 2D par différences finies du modèle de Schlögl. Représentation en fausses couleurs de la concentration $Z(x,t)$. Domaine $500 \times 500$ avec limites périodiques. $Z(x, t=0) \approx 0.7556$. Paramètres: $k_{0}\ a = 0.002$, $k_{1} = 0.039$, $k_{2} \ b = 0.07125$, $k_{3} = 0.030625$, $K_{r} = 20.0$.
Figure: Simulation 3D par différences finies du modèle de Schlögl. Structure binaire: concentration $Z(x,t) > 1.45$. Domaine $250^3$. $K_{r} = 30.0$. Autres paramètres: voir Figure III-13.

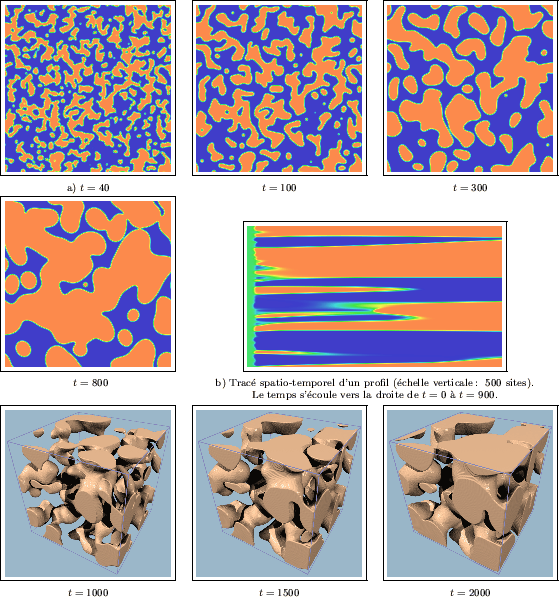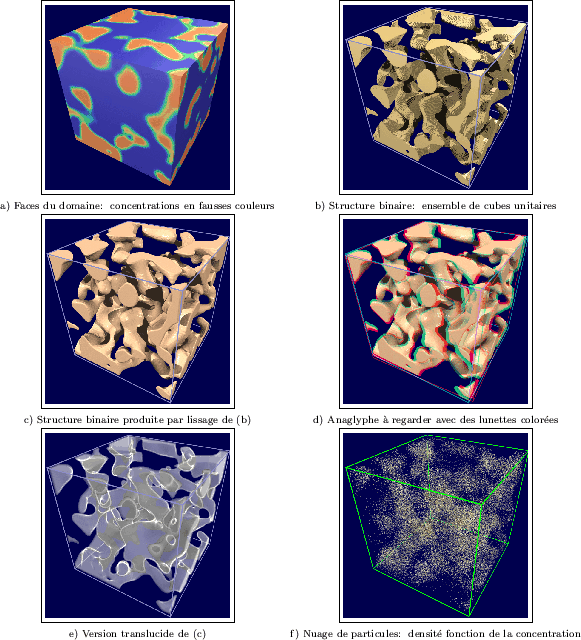
En dimension trois, les structures produites et leurs modes d'évolution sont similaires. La Figure III-14 montre une réalisation du modèle, après seuillage et lissage des régions appartenant à l'une des phases. Des simulations de milieux poreux peuvent ainsi être obtenues. Ce premier modèle nous fournit aussi l'occasion de comparer différents types de visualisations tri-dimensionnelles. Pour une même image de concentrations (valeurs continues), la Figure III-15 montre les résultats obtenus lorsque seules les faces sont représentées (a), puis par seuillage lorsque l'on transforme le milieu en un ensemble de cubes unitaires (b). Un lissage additionnel (c) conduit au mode de représentation que nous adopterons le plus souvent. Grâce à une paire de lunettes filtrantes (rouge/cyan), l'image (d) produira un effet de relief par vision stéréo de (c). Enfin, les représentations (e) et (f) correspondent à d'autres tentatives obtenues dans le cadre de la recherche de méthodes pour observer convenablement les structures générées par la version tri-dimensionnelle d'un modèle.

Figure: Modes de visualisation d'un milieu 3D généré par réaction-diffusion (modèle de Schlögl, $t = 200$). Rendus obtenus par lancer de rayon au moyen du logiciel POVRay.

Mesures
Pour estimer les caractéristiques morphologiques d'un modèle, des mesures spatiales peuvent être réalisées, telles que des granulométries, ou encore la covariance des concentrations. Afin d'obtenir des résultats significatifs, il est nécessaire de déterminer leurs valeurs moyennes grâce à des séries de simulations qui différent uniquement par les séquences de nombres aléatoires utilisés - plus précisément, par les germes introduits pour initialiser un générateur de nombres pseudo-aléatoires. Dans le cas présent, ce générateur est fondé sur la méthode bien connue des congruences; son arithmétique sur $48$ bits doit permettre de limiter les effets indésirables de périodisation (de corrélation) entre les valeurs pseudo-aléatoires. Par ailleurs, dans les modèles aléatoires de réaction-diffusion qui sont traités, seule l'initialisation des concentrations fait appel à une variable aléatoire afin d'obtenir le bruit blanc déjà mentionné. En raison du volume trop important de calculs à réaliser, il ne sera pas possible de donner des mesures moyennes dans le cas de simulations tri-dimensionnelles. En effet, les temps de calculs des mesures représentent souvent une part bien plus grande que les simulations elles-mêmes.


La fonction d'auto-covariance d'une image $Z_{i}$ de concentrations (nombres flottants) est donnée par:

$$E(Z_{i}(x,t) Z_{i}(x+h,t))$$ (III.-18)

Cette expression permet de mettre en valeur l'existence d'une corrélation spatiale entre des concentrations distantes de $h$ unités dans une direction fixée; elle peut être centrée afin qu'elle tende vers zéro en l'absence de corrélation spatiale, soit :

$$E(Z_{i}(x,t) Z_{i}(x+h,t)) - E(Z_{i}(x,t)) E(Z_{i}(x+h,t))$$ (III.-19)

Enfin, la covariance est normalisée (divisée par sa valeur pour $h = 0$, c'est à dire la variance de $Z_{i})$ , de sorte que l'on puisse comparer ses valeurs entre différents modèles, ou encore à différents temps $t$ pour un même modèle. Finalement, on mesurera la covariance centrée et normalisée, ou fonction d'autocorrélation :

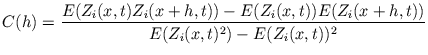$$C(h) = \frac{E(Z_{i}(x,t) Z_{i}(x+h,t)) - E(Z_{i}(x,t)) E(Z_{i}(x+h,t))}{E(Z_{i}(x,t)^{2}) - E(Z_{i}(x,t))^{2}}$$ (III.-20)

pour $h$ variant par pas de $1$ entre 0 et - en général - le tiers de la dimension du domaine dans la direction de mesure.

Lorsque le milieu mesuré est isotrope, la mesure de la covariance peut être réalisée dans une direction quelconque (du point de vue pratique, selon l'une des directions principales de la trame). La fonction d'auto-covariance d'un modèle aléatoire permet en partie de caractériser les structures qu'il renferme. Il est ainsi possible de distinguer plusieurs échelles ou niveaux de structures différentes, ou encore de mettre en évidence leur périodicité le cas échéant.

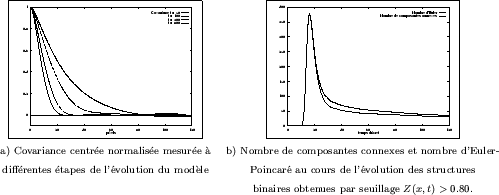
Dans le cas du modèle de Schlögl, la covariance a été mesurée sur 20 réalisations bidimensionnelles, semblables à celle qui est présentée sur la Figure III-13. Ses valeurs moyennes sont données sur la Figure III-16, pour différentes étapes de l'évolution du modèle. D'une part, la portée de la covariance correspond à la valeur de $h$ pour laquelle $C(h)$ atteint son seuil en zéro. En l'absence de seuil, la valeur de $h$ pour laquelle $C(h)$ s'annule pour la première fois pourra définir une portée (en présence d'oscillations par d'exemple). Elle indique la taille moyenne des structures; on vérifie ainsi le changement d'échelle déjà constaté visuellement, soit la croissance des structures. D'autre part, l'aspect des courbes de covariance indique qu'il s'agit d'un modèle plutôt simple, sans phénomènes de répulsion ou de périodicité. La distribution des tailles des grains est régulière.

Pour ce modèle, deux autres mesures ont été réalisées:

Le nombre de composantes connexes constitue également une caractéristique intéressante. Cette mesure est réalisée sur un ensemble binaire, facilement obtenu après seuillage des concentrations. Elle dépend donc fortement de l'intervalle de concentrations sélectionné, pour lequel il existe une infinité de choix possibles, conduisant a priori à des résultats totalement différents. Cependant, nous étudions des milieux qui sont presque biphasés; dans ce cadre, un seuillage qui permet de séparer clairement les deux phases nous semble le seul choix pertinent.

Soit une image binaire formée de grains (valeurs 1) et de vides (valeurs 0). Pour rappel, le nombre de composantes connexes correspond au nombre de grains séparés. Il est déterminé par le balayage de l'image associé au marquage de chaque composante au moyen d'un parcours (ou identification) de tous les pixels (ou voxels) qui en font partie. Lorsqu'un pixel, à valeur 1 et non marqué, est rencontré, une nouvelle composante est ainsi détectée. Une simple file d'attente de "pixels à visiter" permet un parcours "en largeur d'abord" de tous les pixels qui en font partie. Chaque pixel visité est marqué (du numéro de la composante), puis tous ses proches voisins non visités sont placés dans la file. Dans une image, les relations de voisinage entre pixels (voxels) sont fixées; elles caractérisent la connexité de sa trame, ou graphe de voisinage. A trois dimensions, chaque voxel pourra par exemple disposer de $6$ voisins (d'autres connexités possibles sont $12$ ou $26$). Ce type d'algorithme est issu de la théorie élémentaire des graphes. Il s'adapte aisément aux images dont les conditions aux limites sont périodiques, puisqu'il est fondé sur le voisinage immédiat de chaque point.


Le nombre d'Euler-Poincaré est une caractéristique topologique souvent associée aux composantes connexes; il indique le genre d'une structure quelconque, c'est à dire à quelle forme (sphère, tore, etc...) cette structure est homéomorphe (lorsqu'elle est déformée). En deux dimensions, on le détermine par le nombre de composantes connexes (valeur 1) réduit du nombre de "trous". Le nombre de "trous" est donné par le nombre de composantes connexes du vide (valeur 0) moins un. Cependant, lorsque les conditions aux limites d'une image sont périodiques, les structures bidimensionnelles étudiées s'inscrivent dans un espace tri-dimensionnel à topologie torique; dans ce cas, il en résulte que la formule décrite ci-dessus est erronée (elle reste intéressante du point de vue de la signification du nombre d'Euler-Poincaré). Une méthode plus générale consiste à décrire la structure considérée sous la forme d'un maillage (sommets, arêtes, surfaces, ...) construit sur la grille associée à l'image. Le nombre d'Euler-Poincaré est alors donné par:

$$E \ = \ nombre( ) \ - \ nombre( ) \ + \ nombre( ) \ - \ nombre( )$$ (III.-21)

En deux dimensions, $nombre(volumes)$ est égal à zéro et $nombre(surfaces)$ est égal au nombre de pixels à valeur $1$. Cette formule s'applique sans difficultés lorsque les conditions aux limites sont périodiques; il suffit d'en tenir compte lors de la construction du maillage.


Sur le même ensemble de 20 réalisations, ces deux grandeurs ont été mesurées (voir Figure III-16); elles varient essentiellement au cours de la génèse des structures (pour $t < 100$ itérations). Pour $t < 20$, leur comportement est lié au seuil de concentration choisi. Tout d'abord, le seuillage produit un milieu vide; puis le franchissement du seuil est à l'origine d'un pic important du nombre de composantes connexes, dont l'intensité est renforcée par les irrégularités des concentrations à faible échelle. La fusion très rapide de petites structures se traduit ensuite par une très forte diminution du nombre de composantes, entre $t = 20$ et $t = 40$. Cette diminution se poursuit beaucoup plus lentement alors que les structures se sont déjà bien organisées dans l'espace: on peut ainsi distinguer deux étapes. Au cours de la deuxième étape, la coalescence est très limitée; le nombre de composantes diminue parce que les structures dont la taille est trop faible disparaissent lentement. La fusion des structures est à l'origine de "trous" qui sont progressivement comblés pour les mêmes raisons: chaque région (de l'une ou l'autre des phases) a une influence proportionnelle à sa taille, donc à la quantité de matière réactive qu'elle contient. La différence entre le nombre d'Euler-Poincaré et le nombre de composantes connexes est ainsi maximale à la fin de la première étape de coalescence, puis elle diminue lentement.

Figure: Mesures moyennes obtenues à partir de 20 simulations 2D du modèle de Schlögl. Paramètres: voir Figure III-13.

suivant: 4.4 Instabilité de Turing   remonter: 4. Simulations macroscopiques par   précédent: 4.2 Visualisations   [Table des matières]

Decker, Luc. "Modèles de structures aléatoires de type réaction-diffusion". PhD diss. (191 p.), Paris, ENSMP-CMM, 1999.