Modèles de Structures Aléatoires de Type Réaction-Diffusion - Thèse de Morphologie Mathématique - Luc Decker, Ecole des Mines de Paris (1999)

suivant: 2.2 Simulation de la   remonter: 2. Construction du modèle   précédent: 2. Construction du modèle   [Table des matières]

2.1 Modélisation de gouttelettes dans le cadre d'un gaz sur réseau

2.1.1 Principes

Dans une première approche, nous aurions souhaité modéliser une gouttelette comme un simple ensemble de particules, mis en forme et entouré d'espace vide. Chaque particule y représente une fraction de la matière totale dont la gouttelette est constituée, soit -en général- un total de quelques milliers de particules. La cohésion de l'ensemble - en d'autres mots, la conservation de sa forme - pourrait être assurée par l'action d'une force d'attraction entre particules.

Or, dans les modèles courants de Gaz de Réseau, la densité en particules tend essentiellement à s'uniformiser sur toute l'étendue du champ de simulation. Toutefois, il arrive que cette uniformisation ne s'effectue que localement en présence de conditions aux limites particulières, comme dans le cas d'un écoulement contrarié par un obstacle. De fait, la quantité de particules présentes dans une région du réseau est assimilable à une pression. Pour mettre en évidence les capacités hydrodynamiques des modèles de Gaz sur Réseau, une expérience classique consiste ainsi à simuler la propagation et l'amortissement d'une onde de sur-pression [Margolus86]. Citons aussi les expériences de diffusion d'un fluide au travers d'un milieu granulaire hétérogène [Jeulin92a] : des canaux de traversée préférentielle du milieu apparaissent spontanément, en réponse aux augmentations de pression locales provoquées par la présence des obstacles. Une autre conséquence va nous intéresser plus directement: il semble presque exclu que de fortes discontinuités spatiales de la densité en particules puissent être conservées durant toute la durée d'une simulation. C'est ainsi qu'il s'avère irréalisable de maintenir une gouttelette formée de matière dense au milieu d'un espace vide de particules, à plus forte raison si cette gouttelette doit être mise en mouvement. Afin d'illustrer ce point crucial dans la construction du modèle, la Figure IV-6 montre l'évolution d'un système dans lequel on a initialement placé une gouttelette beaucoup plus dense que le milieu qui l'entoure. Il apparait nettement qu'une éventuelle force de cohésion ne saurait s'opposer suffisamment à l'éclatement de la goutte, qui résulte de fortes différences de pression. De plus, dans cette expérience, l'espace entourant la goutte n'était pas totalement vide de particules; à défaut, des effets de trame auraient fait perdre tout caractère physique à la propagation de la sur-pression. La diffusion d'un tel ensemble de particules dans un espace vide génère des fronts quasi-alignés sur les directions principales du réseau (dans le cas du modèle FHP, on obtient ainsi une étoile à six branches), en raison de l'absence de collisions avec des particules en provenance des autres régions du réseau.

Dès lors, la modélisation de gouttelettes dans un Gaz sur Réseau va s'appuyer sur la notion de milieu environnant, qui sera appelé gaz porteur dans notre contexte. En conséquence de nos remarques préliminaires, la densité en particules $d$ de ce gaz porteur devra de plus être égale ou très proche de celle des gouttelettes. Parallèlement, il en résulte aussi que deux catégories - ou phases - de particules sont à présent nécessaires de manière à ce que l'on distingue une gouttelette du gaz porteur environnant; ces phases seront notées $\cal R$ (rouge) et $\cal B$ (bleu) respectivement. Mais dans la pratique, il apparait intéressant de pouvoir simuler le comportement de gouttelettes qui sont formées d'un mélange de différentes espèces chimiques. Toutes ces espèces appartiennent bien sûr à la phase $\cal R$, d'où une distinction entre la phase (ou couleur) et l'espèce chimique (ou label) d'une particule. Par le même principe, on pourra aussi disposer de gouttelettes qui sont constituées chacune d'une espèce chimique unique. Des gouttelettes bien distinctes pourront ainsi se trouver simultanément dans le champ de simulation, le label des particules se confondant avec le label de la gouttelette à laquelle elles appartiennent. Si des propriétés différentes sont ensuite attribuées à chaque gouttelette, la variabilité d'une population hétérogène de gouttelettes pourra être prise en compte.

2.1.2 Le modèle de Gaz sur Réseau Immiscible (ILG)

La stabilité des gouttelettes est essentielle: il s'agit en effet de maintenir une séparation permanente entre les particules issues du gaz porteur et celles provenant des gouttelettes. L'action d'un mécanisme de cohésion doit cependant laisser les gouttelettes libres de répondre aux contraintes extérieures qui leur sont appliquées, telles qu'un champ de forces, ou encore la présence d'obstacles solides. Celles-ci vont ainsi pouvoir se déplacer, se déformer, et éventuellement même coalescer. Pour cet aspect de la modélisation, nous allons partiellement nous appuyer sur le modèle de Gaz sur Réseau Immiscible - en anglais: Immiscible Lattice Gas (ILG) - introduit par Rothman et Keller en 1988 [Rothman88]. Il a en effet été montré que ce modèle peut reproduire l'action d'une tension de surface entre particules réparties entre deux phases. Par rapport à un Gaz sur Réseau usuel, les modifications apportées concernent uniquement l'opérateur de collision $C$; nous en résumons ici les principes et apportons quelques indications quant à leur mise en oeuvre [Decker97].

-

Gaz sur Réseau multi-espèces : situation ordinaire
Lorsque, en un noeud du réseau, une collision implique un ensemble de particules qui appartiennent à $N$ espèces différentes, il y a redistribution aléatoire des espèces (ou labels) associées aux particules, compte tenu des nouvelles positions des particules après résolution de la collision selon les règles standard - par exemple, celles du modèle FHP. Le résultat de l'opérateur de collision est ainsi totalement indépendant des espèces chimiques, donc également des catégories de particules. Un exemple d'une telle situation est présenté sur la Figure IV-7a. A ce sujet, remarquons aussi que la procédure de redistribution est bien peu avantageuse du point de vue de la complexité des calculs. Lorsque le nombre d'espèces $N$ est important, il est effet totalement impossible de précalculer une liste de configurations résultantes et de sélectionner aléatoirement l'une d'elles. L' algorithme qui détermine une configuration acceptable doit alors être appliqué en tout site, à chaque itération : il s'agit d'effectuer des tirages aléatoires successifs, "sans remise". La liste des espèces à placer (présentes avant la collision) est tout d'abord établie; pour chaque particule, on attribue ensuite l'une des espèces tirée au hasard, qui est simultanément retirée de la liste. La procédure est itérée jusqu'à ce qu'il ne reste plus qu'une seule espèce à attribuer à l'unique particule restante.

-

Cas d'un Gaz sur Réseau Immiscible biphasé
Supposons que ce modèle fasse intervenir $k$ espèces de particules, réparties en deux phases ou couleurs - notées $\cal R$ et $\cal B$ comme précédemment. L'opération de redistribution aléatoire des espèces est à présent dirigée par un tirage aléatoire préalable parmi un ensemble restreint de configurations acceptables, qui associent directement positions et phases des particules. Plus précisément, les positions des particules colorées vont être attribuées en fonction du champ local de couleur. Ce champ, noté $F(x)$, est déterminé à chaque instant et en tout noeud $x$ du réseau par les couleurs des particules aux noeuds $(x + c_{i})$ qui appartiennent au voisinage immédiat de $x$. Soit:

$$F(x) = \sum_{i} c_{i} \sum_{j} [ r_{j}(x + c_{i}) - b_{j}(x + c_{i}) ]$$ (IV.-1)

où - de manière générale - $r_{i}(x)$ et $b_{i}(x)$ correspondent au nombre de particules, rouges (de type $\cal R$) ou bleues (de type $\cal B$) respectivement présentes dans la cellule $i$ d'un noeud $x$. En vertu du principe d'exclusion des Gaz sur Réseau, on trouve au plus une particule par cellule, d'où $r_{i}(x) + b_{i}(x) \in \{0,1\}$.
Par convention, on affecte dans ces calculs une pondération $+1$ aux particules de type $\cal R$, et $-1$ aux particules de type $\cal B$.

Par ailleurs, on considère l'ensemble des configurations résultantes possibles pour le noeud $x$, soit $(r'_{i}(x), b'_{i}(x))$. Ces configurations doivent d'une part respecter deux contraintes élémentaires: la conservation du nombre total de particules dans chaque phase, soit:

$$n_{\cal R}(x) = \sum_{i} r_{i}(x) = \sum_{i} r_{i}'(x) \ \ \ et \ \ \ n_{\cal B}(x) = \sum_{i} b_{i}(x) = \sum_{i} b_{i}'(x)$$ (IV.-2)

ainsi que la conservation de la quantité de mouvement totale en $x$ :

$$\sum_{i} c_{i}(r_{i}(x) + b_{i}(x)) = \sum_{i} c_{i}(r_{i}'(x) + b_{i}'(x))$$ (IV.-3)

D'autre part, chaque configuration possible est caractérisée par le flux local de couleur $q$ qu'elle susceptible d'engendrer, donné par:

$$q[r'(x),b'(x)] = \sum_{i} c_{i}[r_{i}'(x) - b_{i}'(x)]$$ (IV.-4)

Finalement, le résultat de l'opérateur de collision pour le modèle ILG est donné par un tirage aléatoire parmi l'ensemble des configurations $(r'_{i}(x), b'_{i}(x))$ qui minimisent le travail $W$ du flux de couleur $q$ contre le champ local $F$, soit

$$W = - F(x) \cdot q[r'(x),b'(x)]$$ (IV.-5)

Il reste encore à placer aléatoirement les espèces chimiques - selon une procédure semblable à celle décrite dans le cas habituel d'un Gaz sur Réseau multi-espèces. Cependant, les positions autorisées sont largement restreintes par la connaissance de la phase associée à chaque espèce, alors que les positions des phases sont à présent fixées. Cette séquence d'opérations a pour principal effet de regrouper spatialement les particules de même phase; elle est illustrée par un exemple simple d'une collision entre deux particules sur la Figure IV-7b. Pour ce modèle, il est important de noter que les couleurs des particules présentes en un noeud vont d'elles-même déterminer quelles règles de collision peuvent être déclenchées, et qu'en conséquence elles vont fixer les positions finales des particules après collision.

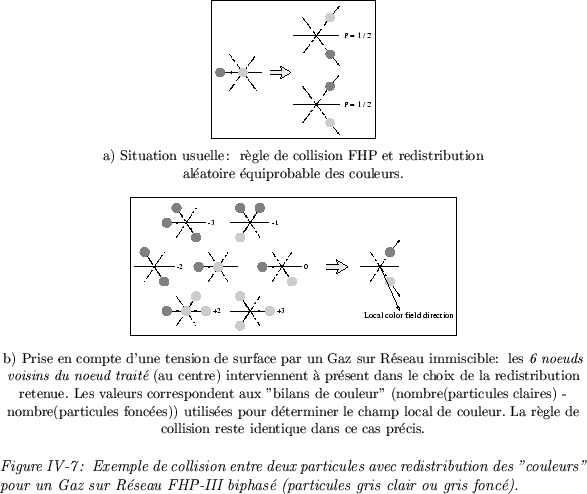
En pratique, toutes les configurations minimales du modèle ILG sont pré-calculées et enregistrées dans une table à accès direct indexé (en anglais: look-up table). Au cours des simulations, les calculs des collisions sont donc réalisés par une simple lecture de cette table. Le champ de couleur $F$ est représenté sous la forme d'un vecteur de coordonnées entières, qui est obtenu par projections selon deux directions principales du réseau. Une table préliminaire de type "arc-tangente" est appelée de façon à convertir le vecteur $F$ en une valeur discrète proportionnelle à un angle avec une précision donnée - par exemple, pour une précision de 3 degrés: l'intervalle des entiers entre 0 et $119$ inclus - soient 120 secteurs angulaires. Une table principale fournit directement la liste des configurations minimales, c'est à dire des paires de valeurs représentant le codage binaire des positions des particules pour chacune des deux phases. Il ne reste alors qu'à sélectionner aléatoirement l'une d'elles. La clé d'accès de la table principale (c'est à dire la technique d'indexation) utilise un codage binaire sur 17 bits, par concaténation des informations suivantes: positions des particules avant collision (7 bits), nombre de particules appartenant à la phase $\cal R$ (3 bits), et direction angulaire du champ $F$ (7 bits). Les valeurs des clés sont dans la pratique comprises entre $131$ et $122751$, cette borne supérieure fixant la dimension de la table. Il aurait été possible de comprimer davantage les informations puisque il n'existe que $38520$ configurations utiles, les autres entrées de la table correspondent à des configurations impossibles et restent donc vides. Cependant, le codage adopté pour les accès directs aux configurations semble un bon compromis entre l'espace mémoire nécessaire et la vitesse de calcul. Par ailleurs, nous avons constaté qu'un excès de précision était préjudiciable à la qualité du résultat final: un faible taux d'erreur entraîne un bruit blanc qui va estomper les effets de la forte discrétisation des calculs. En fait, des erreurs bien plus importantes sont commises en raison de la géométrie du réseau et des effets de trame apparaissent lorsque la sélection des configurations résultantes est totalement déterministe. Cette observation concerne aussi bien la précision de la direction angulaire du champ $F$ que le calcul des configurations. Lorsque les résultats de l'opérateur de collision sont pré-calculés, un écart est toléré afin de retenir un ensemble plus large de configurations qui sont proches de minimiser $W$ (une autre solution consisterait à réduire directement le nombre de secteurs angulaires).

Le modèle de Gaz sur Réseau Immiscible a été appliqué avec succès à divers systèmes, en particulier afin de s'assurer qu'il était effectivement à l'origine d'une tension de surface [Rothman88]. Il a également été mis en oeuvre pour vérifier qu'il conduisait bien à un phénomène de décomposition spinodale [Rothman89]. Il s'agit d'observer la dynamique d'un mélange initialement hétérogène de deux phases incompatibles: le système va évoluer lentement, tel une émulsion, pour former spontanément un ensemble de régions homogènes constituées uniquement de l'une des deux phases. Tandis que leur nombre diminue, la surface des régions augmente régulièrement par fusions successives (coalescence) de régions homogènes plus petites. Ces régions constituent par ailleurs des structures aléatoires intéressantes. Nous avons reproduit cette expérience afin de valider notre implantation du modèle ILG; la Figure IV-8 en présente les résultats, qui sont conformes à ceux obtenus par Rothman et Zaleski.

2.1.3 Application du modèle ILG

Dans le cadre de notre étude, nous avons recours au modèle ILG dans le seul but de conserver la cohésion de gouttelettes déjà formées et placées en l'état dans un champ de simulation bidimensionnel. En général, il s'agira de disques de rayon variable $r$, mais il serait immédiat de leur donner une autre forme. En effet, même si l'action de la tension de surface tend à produire des gouttes parfaitement rondes, cette évolution est d'autant plus lente que le rayon de courbure de l'interface gouttelette-gaz porteur est important. Il reste donc possible d'introduire des gouttelettes de forme quelconque dans le système, sous réserve que leurs contours soit arrondis. Enfin, la taille des gouttelettes joue également un rôle: un diamètre insuffisant ($r < 10$ unités) semble nuire à leur stabilité.

Pour rappel, la densité en particules $d$ des gouttelettes et celle du gaz porteur doivent être égales. D'autre part, le mécanisme de cohésion du modèle ILG s'exerce pleinement lorsque le nombre de collisions entre particules est élevé, donc lorsque la densité $d$ est suffisamment importante - soit environ $d \geq 0.50$ particule/cellule selon les expériences de stabilité qui ont été réalisées. Il en résulte une viscosité assez grande des fluides simulés, qui ne peut être évitée.

L'introduction d'une gouttelette dans le système est réalisée par un simple changement de phase $\cal B \rightarrow \cal R$ - autrement dit, une colorisation - de toutes les particules présentes dans une région bien délimitée du réseau, ayant la forme souhaitée. Ni les vitesses des particules, ni leur densité se sont modifiées: cette opération ne perturbe aucunement l'évolution du modèle.

suivant: 2.2 Simulation de la   remonter: 2. Construction du modèle   précédent: 2. Construction du modèle   [Table des matières]

Decker, Luc. "Modèles de structures aléatoires de type réaction-diffusion". PhD diss. (191 p.), Paris, ENSMP-CMM, 1999.