Modèles de Structures Aléatoires de Type Réaction-Diffusion - Thèse de Morphologie Mathématique - Luc Decker, Ecole des Mines de Paris (1999)
Le modèle des points poissonniens n'est pas - au sens strict - un
modèle aléatoire à grains primaires. Il est cependant à la base de
la plupart des autres modèles. Pour rappel, il s'agit d'une réalisation
de points aléatoires indépendants vérifiant une distribution spatiale
uniforme avec une densité 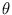 . Cette réalisation peut être enregistrée
dans une image digitale binaire. Les points poissonniens constituent les
positions d'implantation des grains primaires pour les modèles qui suivent.
Par ailleurs, ce modèle très simple est également utilisé
pour simuler des particules en suspension, ou encore les positions
de germes dans un modèle de germination-croissance tel que les polyèdres
de Voronoï mis en oeuvre au chapitre suivant.
. Cette réalisation peut être enregistrée
dans une image digitale binaire. Les points poissonniens constituent les
positions d'implantation des grains primaires pour les modèles qui suivent.
Par ailleurs, ce modèle très simple est également utilisé
pour simuler des particules en suspension, ou encore les positions
de germes dans un modèle de germination-croissance tel que les polyèdres
de Voronoï mis en oeuvre au chapitre suivant.
Par extension, on construit d'autres modèles de points aléatoires
qui ne vérifient plus une distribution spatiale uniforme, ou pour
lesquels il n'y a plus indépendance entre les positions des points. C'est
le cas du modèle "du noyau dur" (en anglais: hard-core), où une distance
minimale de répulsion est associée à chaque point. Le processus de
simulation de tels points est séquentiel: à chaque point implanté est
associé une région interdite aux implantations de points suivantes.
La régularité de la répartition spatiale des points aléatoires peut ainsi
être étroitement controlée.
L'idée intuitive du schéma booléen réside en un jet aléatoire
de grains primaires. Dans sa version générale, ce modèle a été
construit et étudié par Matheron [Matheron67,Matheron75].
Soit une simulation de points poissoniens 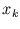 . Un
schéma booléen
. Un
schéma booléen 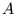 est obtenu par l'implantation par
est obtenu par l'implantation par 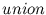 d'un grain primaire aléatoire
d'un grain primaire aléatoire 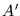 en tout point
en tout point 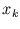 :
:
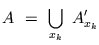 |
(I.-1) |
où
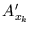 représente le translaté du grain primaire
représente le translaté du grain primaire 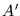 au point
au point 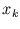 .
.
On génère ainsi un ensemble aléatoire binaire, apte à décrire
des structures biphasées. La Figure I-2 en donne deux exemples.
Une fonction aléatoire booléenne (F.A.B.) représente l'équivalent
du schéma booléen (binaire) pour un modèle aléatoire numérique.
Ce modèle a été initialement introduit par Jeulin pour la simulation
de surfaces rugueuses [Jeulin81]. Dans les références [Serra82,Serra88]
sont présentées d'autres applications et extensions.
Une F.A.B. est basée sur un ensemble de fonctions primaires aléatoires 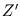 qui sont
implantées par l'opérateur sup sur une réalisation de points poissonniens
qui sont
implantées par l'opérateur sup sur une réalisation de points poissonniens 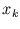 , soit
, soit
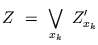 |
(I.-2) |
La valeur finale en tout point d'une réalisation de F.A.B. correspond ainsi
au maximum des valeurs des fonctions primaires qui se recouvrent en ce point.
Les fonctions aléatoires sont usuellement représentées sous la forme d'images
à niveaux de gris. La Figure I-3 montre des réalisations de F.A.B.; ce type
de modèle produit des structures qui ont souvent l'aspect d'agrégats.
Les modèles aléatoires de Feuilles Mortes ont été introduits
par Jeulin en 1980 [Jeulin80,Jeulin81], à partir de travaux plus
anciens de Matheron [Matheron68]. Le processus d'implantation est purement
séquentiel : on simule le recouvrement successif de grains primaires,
d'où l'analogie avec la chute de feuilles mortes qui a donné son nom
au modèle. Lorsque deux feuilles se superposent, c'est la dernière
feuille tombée qui occupe la zone de recouvrement. La valeur finale
en tout point d'une réalisation correspond à celle de la dernière
fonction ou grain primaire qui recouvre ce point.
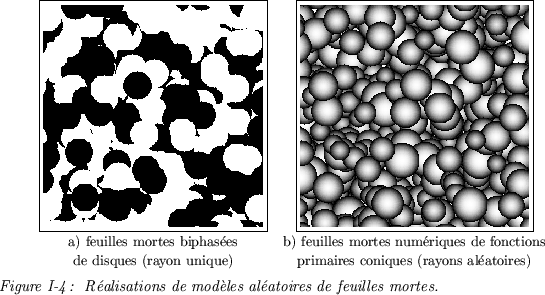
Il existe des modèles multi-phasés de feuilles mortes - appelés
feuilles mortes colorées [Jeulin80] - pour lesquels on implante
des grains primaires appartenant à une phase tirée aléatoirement
(par exemple, des grains noirs ou blancs comme sur la Figure I-4a).
Dans le cas de modèles numériques, les fonctions aléatoires
de feuilles mortes [Jeulin89] rendent
particulièrement bien compte d'une profondeur de champ (Figure I-4b).
Ils sont par exemple adaptés à la simulation de micrographies de
grains de poudres.
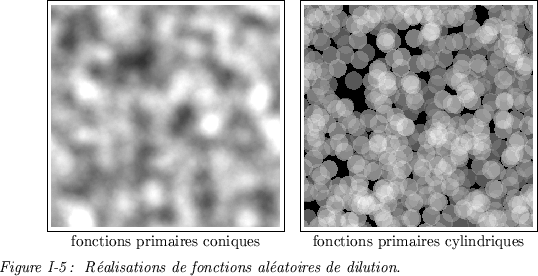
Dans une fonction aléatoire de dilution [Serra68], les fonctions primaires 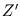 sont implantées par addition, soit
sont implantées par addition, soit
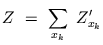 |
(I.-3) |
Si l'on considère les réalisations de ces modèles en tant que surfaces (ou reliefs),
ils s'avèrent bien adaptés aux situations où des empilements statiques de matière ou
d'objets sont observés, sans écoulements ou déplacements ultérieurs à leurs
implantions.
Dans ce modèle introduit par Jeulin [Jeulin91],
les fonctions primaires sont implantées alternativement par
le sup et par l' inf. Pour une application à la
simulation de surfaces rugueuses, ce cycle se décompose ainsi
en une phase d'apport - ou de dépôt - de matière, et une phase
d'abrasion - ou d'érosion. On pourra utiliser des familles de
fonctions primaires différentes pour les deux phases.

Decker, Luc. "Modèles de structures aléatoires de type réaction-diffusion". PhD diss. (191 p.), Paris, ENSMP-CMM, 1999.
![]() représente le translaté du grain primaire
représente le translaté du grain primaire ![]() au point
au point ![]() .
.

![]() qui sont
implantées par l'opérateur sup sur une réalisation de points poissonniens
qui sont
implantées par l'opérateur sup sur une réalisation de points poissonniens ![]() , soit
, soit


 Decker, Luc. "Modèles de structures aléatoires de type réaction-diffusion". PhD diss. (191 p.), Paris, ENSMP-CMM, 1999.
Decker, Luc. "Modèles de structures aléatoires de type réaction-diffusion". PhD diss. (191 p.), Paris, ENSMP-CMM, 1999.